Предмет: Алгебра,
автор: Андрей22122000
предел функции как решить?
Приложения:
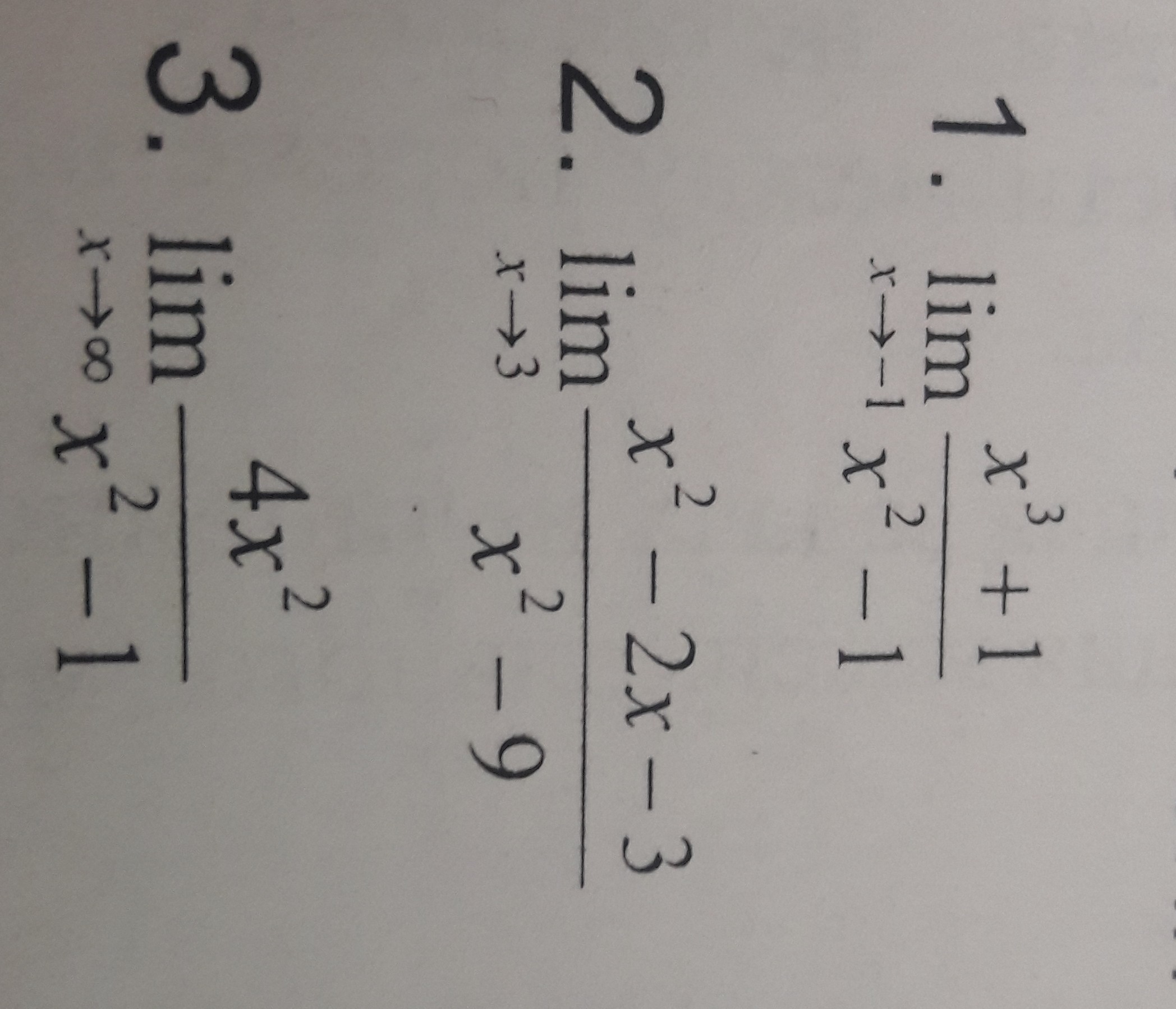
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: География,
автор: nastyashumilovskaya
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: tereb
Предмет: Обществознание,
автор: sve2438