Предмет: Алгебра,
автор: iamolyat
С подробным решением !
Приложения:
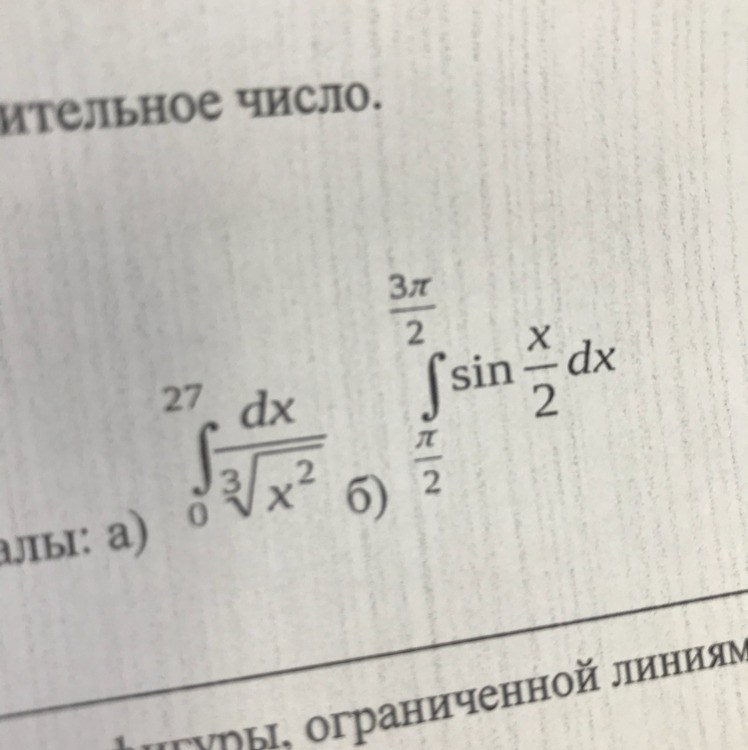
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: torysteller1
Предмет: Геометрия,
автор: ivankarpovich
Предмет: Английский язык,
автор: sarlin11
Предмет: Математика,
автор: НикитаМитюшов236
Предмет: Алгебра,
автор: iac2008