Question

ДАЮ 50 Баллов . Построить график функции : 1) y= 2+3x-x^3 ; 2) y= 6x^4 - 4x^6

Answer 1

ДАНО
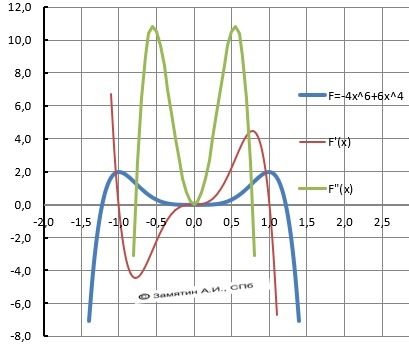
Y= - 4*x⁶ + 6*x⁴
ИССЛЕДОВАНИЕ.
1. Непрерывная -D(x) -  Х∈(-∞;+∞). Вертикальных асимптот - нет
2. Корни функции - пересечение с осью Х; х₁ = 0, x₂ = - √6/2≈ - 1,22,  х₃ = √6/2 ≈ 1,22.
3. Пересечение с осью У - У(0) = 0 .
4. Поведение на бесконечности. У(-∞) = +∞, У(+∞) = +∞. Горизонтальной асимптоты нет.
5 Корни первой производной - точки экстремумов.
  Y"(x) = - 24*x⁵ + 24*x³ = 24*x³*(1-x)(1+x) = 0
Максимум - У(-1) = У(1) = 2. Минимум -  Y(0) = 0
6. Интервалы монотонности .
Возрастает - X∈(-∞;-1]∪[0;1], Убывает - X∈[-1;0]∪[1;+∞).
7. Корни второй производной - точки перегиба.
Y"(x) = - 120*x⁴ + 72*x² = 24*x²*(3/5 - x²) = 0.
x₁ = -  √15/5 ≈ -0.77,  x₂.₃ = 0,  x₄ = √15/5 ≈ 0.77. Внимание - ДВА корня = 0.
8.  
Выпуклая - "горка" - X∈(-∞;-√15/5]∪[√15/5;+∞)
Вогнутая - "ложка" - X∈[-√15/5;√15/5]
9.  У(-х) = У(х) -  функция чётная.
10. График функции в приложении. 
ДАНО
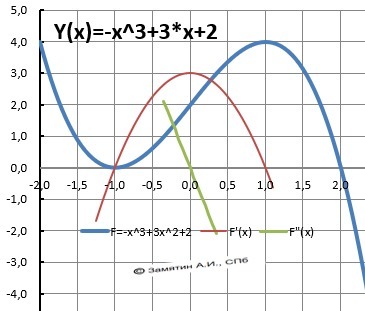
Y= - x³ + 3*x +2
ИССЛЕДОВАНИЕ.
1. Непрерывная -D(x) -  Х∈(-∞;+∞). Вертикальных асимптот - нет
2. Корни функции - пересечение с осью Х; х₁,₂ = 0, х₃ = 0.
3. Пересечение с осью У - У(0) = 2 .
4. Поведение на бесконечности. У(-∞) = +∞, У(+∞) = -∞. Горизонтальной асимптоты нет.
5 Корни первой производной - точки экстремумов.
  Y"(x) = - 3*x² + 3 =3*(1-x)(1+x) = 0
Максимум - У(1) = 4. Минимум -  Y(-1) = 0
6. Интервалы монотонности .
Возрастает медлу корнями - X∈[-1;1], Убывает - X∈(-∞;-1]∪[1;+∞).
7. Корни второй производной - точки перегиба.
Y"(x) = - 6*x = 0.
x₁ = 0.
8.  
Выпуклая - "горка" - X∈[0;+∞),Вогнутая - "ложка" - X∈(-∞;0]
9.  У(-х) = У(х), У(-х)≠ - У(х) -  функция ни чётная ни нечётная.
10. График функции в приложении.