Предмет: Математика,
автор: Аноним
Помогите решить пожалуйста производную сложной функции
Приложения:
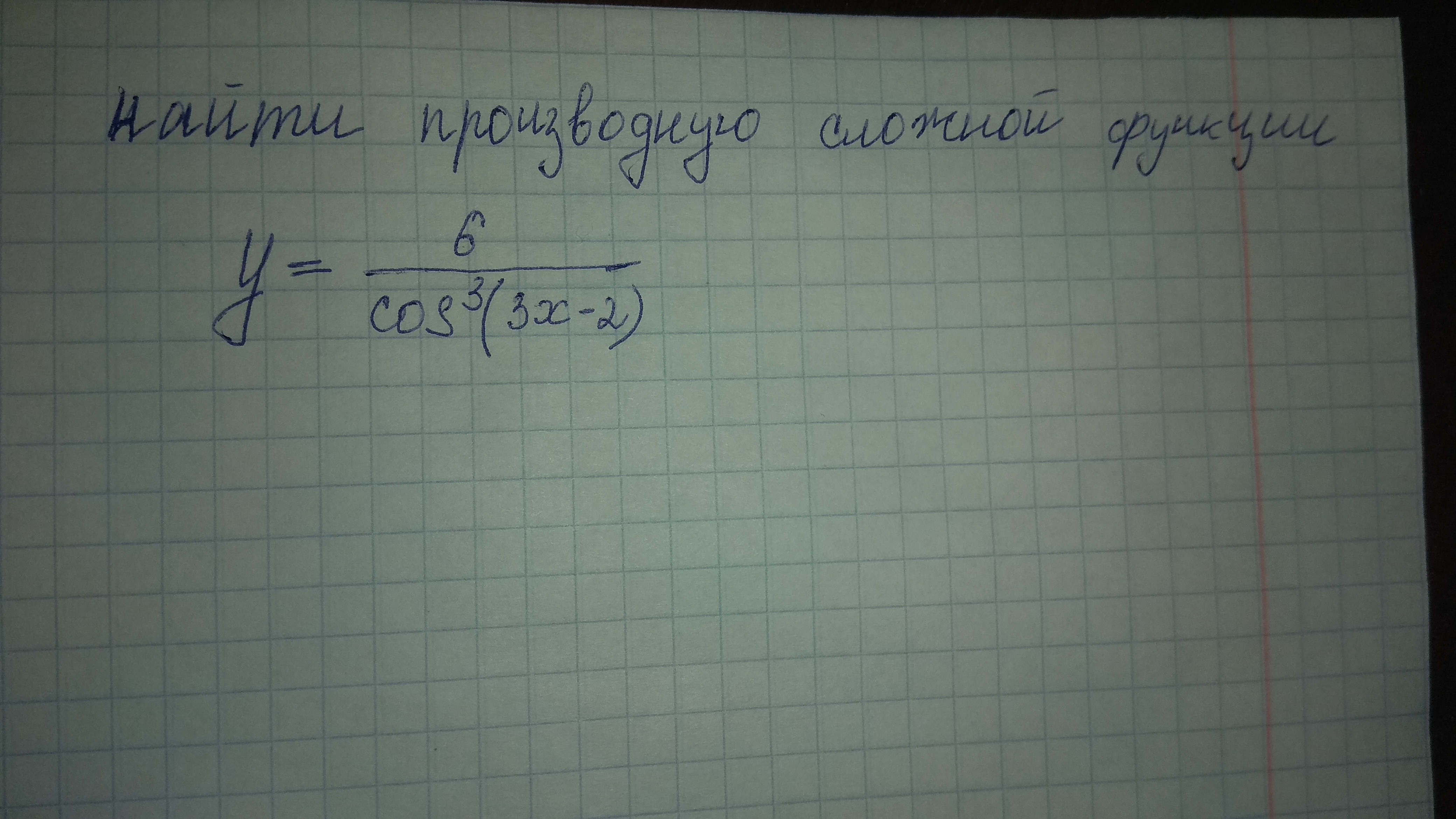
Tanda80:
вроде бы уже решила :)
Ответы
Автор ответа:
3
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: muroslavad89
Предмет: Английский язык,
автор: zrjytfrfyet
Предмет: Биология,
автор: milanakocanova1
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: миша323