Предмет: Алгебра,
автор: Pandaass
Допоможіть будьласка
Приложения:

Ответы
Автор ответа:
1
1) Ответ: Г).
2) Ответ: А).
3) Ответ: Д).

Ответ: В).

Ответ: B) 0<x<3, (0,3) .

Ответ: Б).
7) решено ранее
![8)\; \; log_{0,2}(x^2-2x-3) \geq -1\; ,\\\\ODZ:\; \; x^2-2x-3\ \textgreater \ 0\; ,\; \; x_1=-1\; ,\; x_2=3\; \; (teorema\; Vieta)\\\\+++(-1)---(3)+++\; \; \; x\in (-\infty ,-1)\cup (3,+\infty )\\\\log_{0,2}(x^2-2x-3) \geq log_{0,2}(0,2)^{-1}\; ,\; \; (0,2)^{-1}=(\frac{1}{5})^{-1}=5\\\\t.k.\; 0,2\ \textless \ 1\; ,\; to\; \; \; x^2-2x-3 \leq 5\; ,\\\\x^2-2x-8 \leq 0\; ,\; \; x_1=-2\; ,\; x_2=4\; \; (teorema\; Vieta)\\\\+++[-2\, ]---[\, 4\, ]+++\\\\x\in [-2,4\, ]\\\\ \left \{ {{x\in [-2,4\, ]} \atop {x\in (-\infty ,-1)\cup (3,+\infty )}} \right. \; \; \Rightarrow \underline {x\in [-2,-1)\cup (3,4\, ]} 8)\; \; log_{0,2}(x^2-2x-3) \geq -1\; ,\\\\ODZ:\; \; x^2-2x-3\ \textgreater \ 0\; ,\; \; x_1=-1\; ,\; x_2=3\; \; (teorema\; Vieta)\\\\+++(-1)---(3)+++\; \; \; x\in (-\infty ,-1)\cup (3,+\infty )\\\\log_{0,2}(x^2-2x-3) \geq log_{0,2}(0,2)^{-1}\; ,\; \; (0,2)^{-1}=(\frac{1}{5})^{-1}=5\\\\t.k.\; 0,2\ \textless \ 1\; ,\; to\; \; \; x^2-2x-3 \leq 5\; ,\\\\x^2-2x-8 \leq 0\; ,\; \; x_1=-2\; ,\; x_2=4\; \; (teorema\; Vieta)\\\\+++[-2\, ]---[\, 4\, ]+++\\\\x\in [-2,4\, ]\\\\ \left \{ {{x\in [-2,4\, ]} \atop {x\in (-\infty ,-1)\cup (3,+\infty )}} \right. \; \; \Rightarrow \underline {x\in [-2,-1)\cup (3,4\, ]}](https://tex.z-dn.net/?f=8%29%5C%3B+%5C%3B+log_%7B0%2C2%7D%28x%5E2-2x-3%29+%5Cgeq+-1%5C%3B+%2C%5C%5C%5C%5CODZ%3A%5C%3B+%5C%3B+x%5E2-2x-3%5C+%5Ctextgreater+%5C+0%5C%3B+%2C%5C%3B+%5C%3B+x_1%3D-1%5C%3B+%2C%5C%3B+x_2%3D3%5C%3B+%5C%3B+%28teorema%5C%3B+Vieta%29%5C%5C%5C%5C%2B%2B%2B%28-1%29---%283%29%2B%2B%2B%5C%3B+%5C%3B+%5C%3B+x%5Cin+%28-%5Cinfty+%2C-1%29%5Ccup+%283%2C%2B%5Cinfty+%29%5C%5C%5C%5Clog_%7B0%2C2%7D%28x%5E2-2x-3%29+%5Cgeq+log_%7B0%2C2%7D%280%2C2%29%5E%7B-1%7D%5C%3B+%2C%5C%3B+%5C%3B+%280%2C2%29%5E%7B-1%7D%3D%28%5Cfrac%7B1%7D%7B5%7D%29%5E%7B-1%7D%3D5%5C%5C%5C%5Ct.k.%5C%3B+0%2C2%5C+%5Ctextless+%5C+1%5C%3B+%2C%5C%3B+to%5C%3B+%5C%3B+%5C%3B+x%5E2-2x-3+%5Cleq+5%5C%3B+%2C%5C%5C%5C%5Cx%5E2-2x-8+%5Cleq+0%5C%3B+%2C%5C%3B+%5C%3B+x_1%3D-2%5C%3B+%2C%5C%3B+x_2%3D4%5C%3B+%5C%3B+%28teorema%5C%3B+Vieta%29%5C%5C%5C%5C%2B%2B%2B%5B-2%5C%2C+%5D---%5B%5C%2C+4%5C%2C+%5D%2B%2B%2B%5C%5C%5C%5Cx%5Cin+%5B-2%2C4%5C%2C+%5D%5C%5C%5C%5C+%5Cleft+%5C%7B+%7B%7Bx%5Cin+%5B-2%2C4%5C%2C+%5D%7D+%5Catop+%7Bx%5Cin+%28-%5Cinfty+%2C-1%29%5Ccup+%283%2C%2B%5Cinfty+%29%7D%7D+%5Cright.+%5C%3B+%5C%3B+%5CRightarrow+%5Cunderline+%7Bx%5Cin+%5B-2%2C-1%29%5Ccup+%283%2C4%5C%2C+%5D%7D)
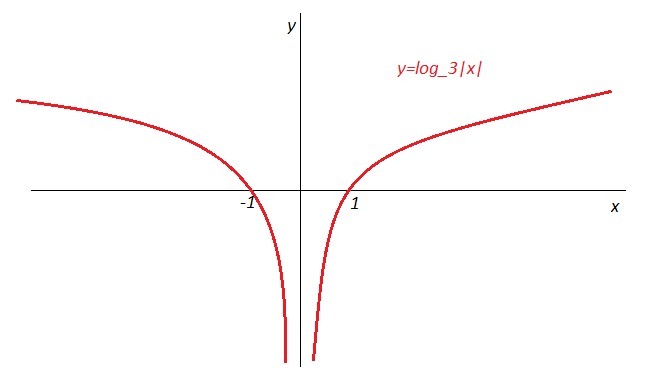
9) см рисунок
2) Ответ: А).
3) Ответ: Д).
Ответ: В).
Ответ: B) 0<x<3, (0,3) .
Ответ: Б).
7) решено ранее
9) см рисунок
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: kiril6969hopk
Предмет: Другие предметы,
автор: kamilaaliyeva26
Предмет: Право,
автор: Dodi05
Предмет: Математика,
автор: Школьник1818
Предмет: Математика,
автор: wolf47