Предмет: Алгебра,
автор: ОгнезвёздБесстрашный
решите систему уравнений под номером 11
Приложения:
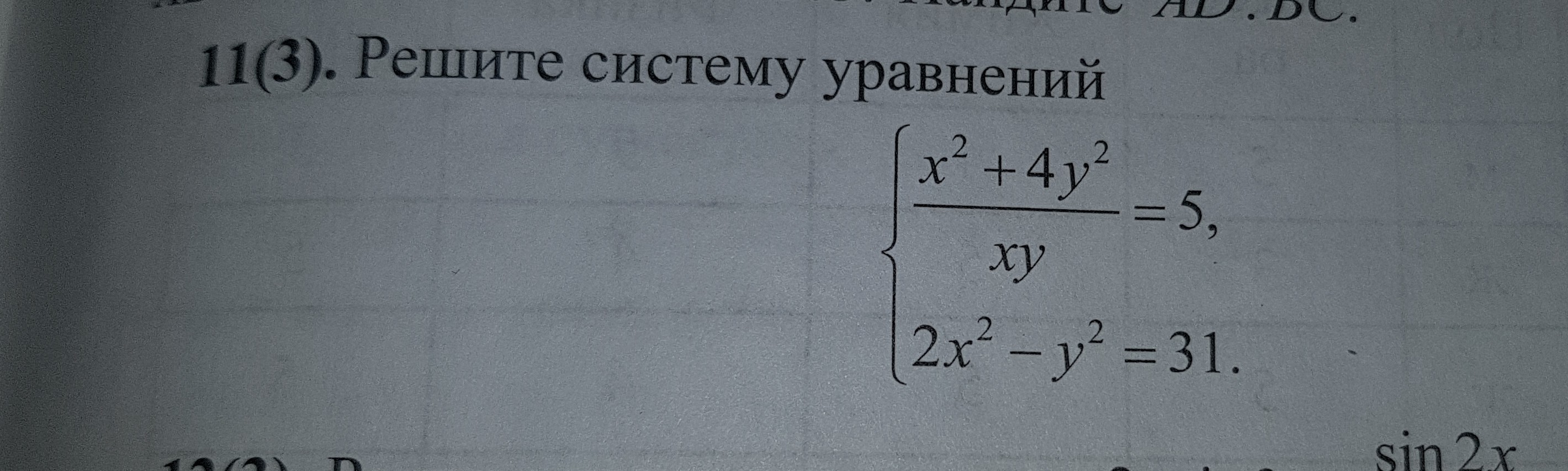
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: shostak1polina
Предмет: Математика,
автор: shjshsjsksj
Предмет: Биология,
автор: sonyanosofia
Предмет: Геометрия,
автор: саша1074
Предмет: География,
автор: kuchinnikita835