Предмет: Математика,
автор: rfghethwterherh
Площадь равнобедренной трапеции равна 96. Диагональ трапеции делит её тупой
угол пополам. Длина меньшего основания равна 3. Найдите периметр трапеции.
NNNLLL54:
42
Ответы
Автор ответа:
7
Если диагональ трапеции делит её тупой угол пополам, то нижнее основание равно боковым сторонам. Примем их равными х.
Средняя линия L трапеции равна: L = (3+х)/2.
Высота Н трапеции равна: Н = √(х² - ((х-3)/2)²) = √(3х²+6х-9)/2.
Площадь S = L*H = 96.
Подставим значения: ((3+х)/2)*(√(3х²+6х-9)/2) = 96.
Если возведём в квадрат обе части уравнения и приведём подобные , то получим уравнение четвёртой степени:

Решение его весьма сложное и даёт результат: х = 13.
Отсюда ответ: периметр равен Р = 3*13 + 3 = 42.
Средняя линия L трапеции равна: L = (3+х)/2.
Высота Н трапеции равна: Н = √(х² - ((х-3)/2)²) = √(3х²+6х-9)/2.
Площадь S = L*H = 96.
Подставим значения: ((3+х)/2)*(√(3х²+6х-9)/2) = 96.
Если возведём в квадрат обе части уравнения и приведём подобные , то получим уравнение четвёртой степени:
Решение его весьма сложное и даёт результат: х = 13.
Отсюда ответ: периметр равен Р = 3*13 + 3 = 42.
Приложения:
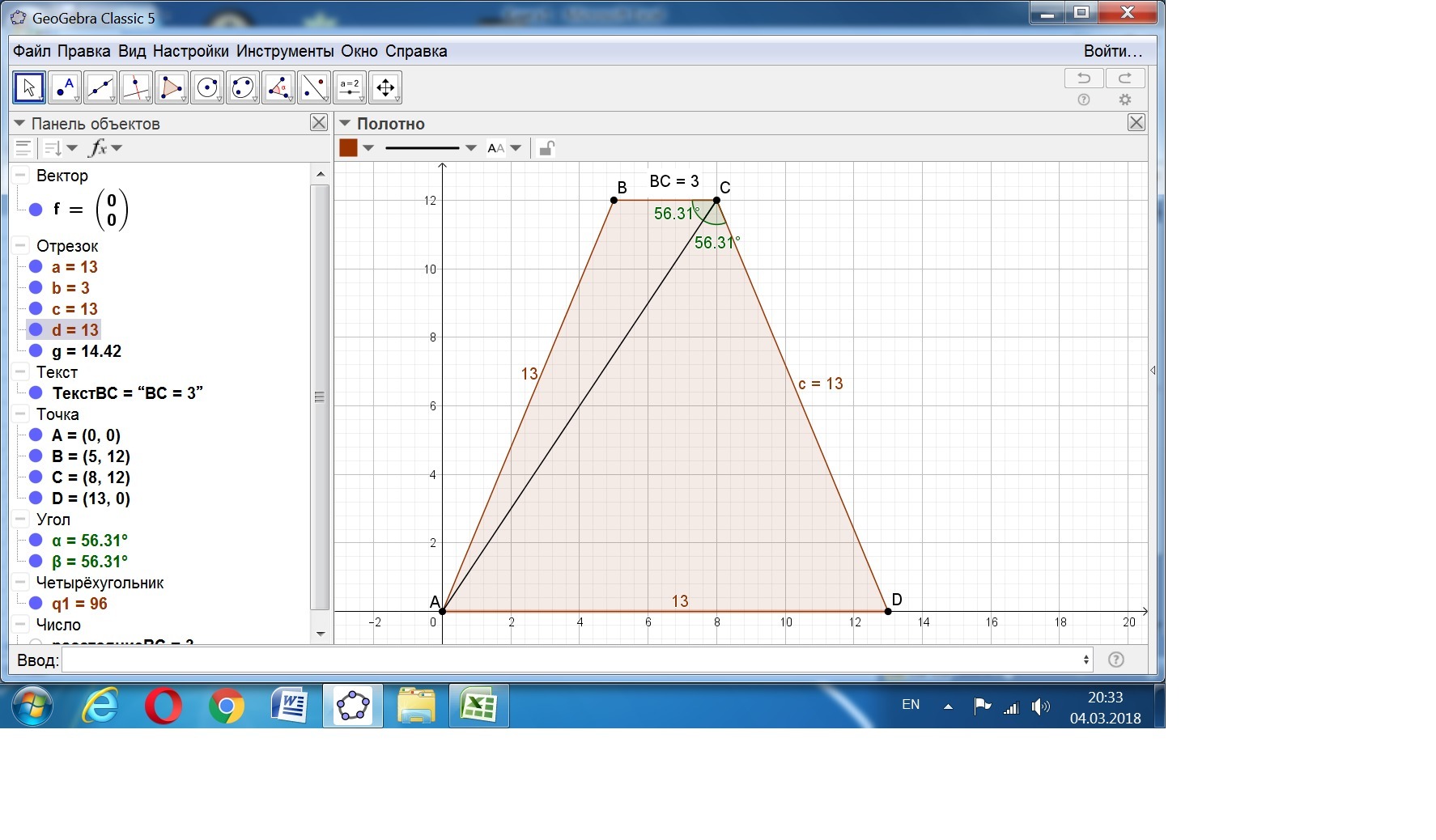
Сложная задача
Какая формула здесь используется Н = √(х² - ((х-3)/2)²) ?
можете подробней обьяснить?
(х-3)/2 это проекция боковой стороны на основание. А высота - по Пифагору.
Похожие вопросы
Предмет: Физика,
автор: obozrevalka888
Предмет: Українська мова,
автор: elizavetalymar02
Предмет: Русский язык,
автор: dmastahov163
Предмет: Литература,
автор: MrKalininMakar
Предмет: Математика,
автор: Яна3636