Предмет: Алгебра,
автор: alinapromop4grz5
ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА!
Мат.анализ (Начальный ур.)
Задание: Найти предел последовательностей при n стремящ. к бесконечности
Приложения:
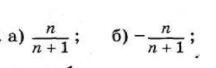
Ответы
Автор ответа:
1
1)

2) Повторить все записи из 1), только сначала вынести знак "-" перед знаком предела

2) Повторить все записи из 1), только сначала вынести знак "-" перед знаком предела
Похожие вопросы
Предмет: Музыка,
автор: arinasamokhina2503
Предмет: Обществознание,
автор: kristinakartasovp405
Предмет: Русский язык,
автор: ruslanibragimov49400
Предмет: Химия,
автор: Drys1999
Предмет: Математика,
автор: sashavekhter