Предмет: Алгебра,
автор: art021220001
Номер 353 (а б в )помогите решить пожалуйста
Приложения:
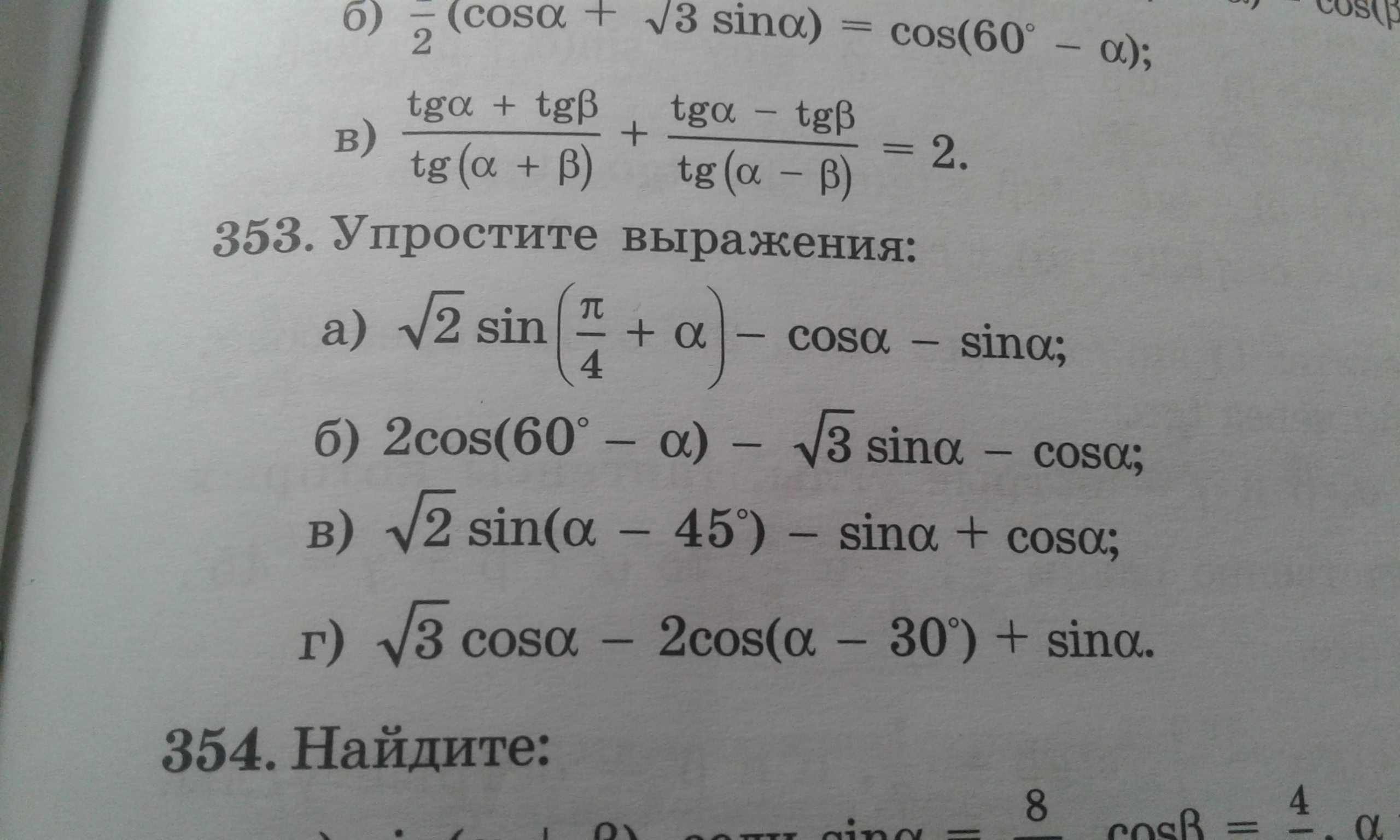
Ответы
Автор ответа:
1
а)

б)

в)

б)
в)
art021220001:
Спасибо большое
Похожие вопросы
Предмет: Биология,
автор: tinairsenko333
Предмет: Английский язык,
автор: inhbhiubhb
Предмет: Информатика,
автор: Jdjdjdkdn
Предмет: Информатика,
автор: olgamallceva
Предмет: Литература,
автор: 46807238