Question

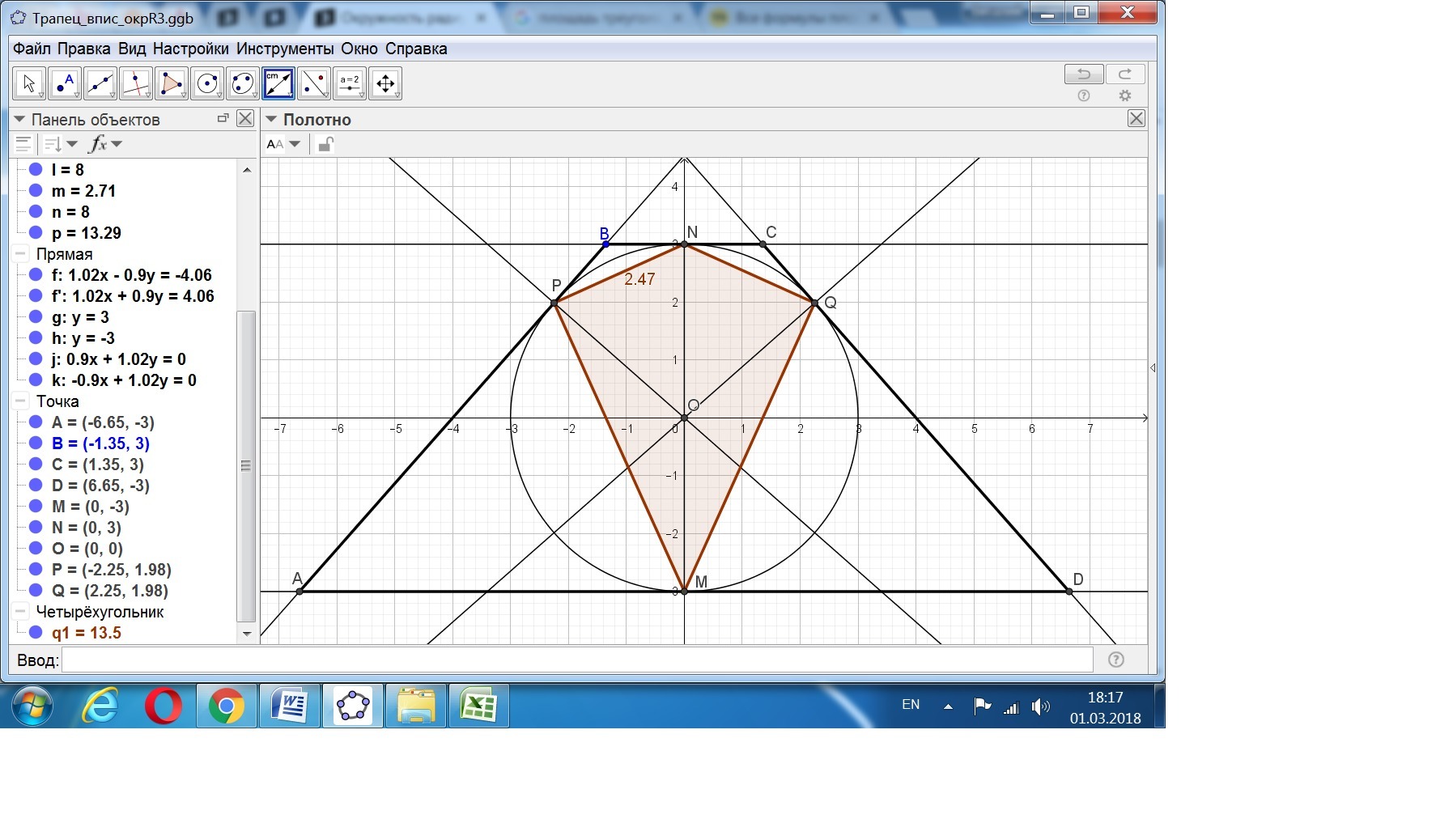
Окружность радиуса 3 вписана в равнобокую трапецию ABCD
(AD || BC), площадь которой равна 48. Окружность касается оснований
в точках M и N и боковых сторон в точках P и Q. Требуется найти площадь четырёхугольника MPNQ.

Answer 1

Средняя линия L трапеции, в которую вписана окружность радиуса R, равна: L = S/(2R) = 48/(2*3) = 8.
Боковая сторона такой трапеции равна средней линии.
Находим синус острого угла А:
sin A = 6/8 = 3/4.
Угол PON, как взаимно перпендикулярный с углом А, равен ему.
Тогда отрезок  PQ равен:
PQ = 2*R*sinA = 2*3*(3/4) =9/2.

Ответ: площадь S четырёхугольника MPNQ равна:
S = (1/2)*6*(9/2) = 27/2 = 13,5.