Предмет: Алгебра,
автор: thg20014
Решите пожалуйста
корень из 2 cos^2x + cos x = 0
Ответы
Автор ответа:
2
Решение в прикрепленном файле.
Приложения:
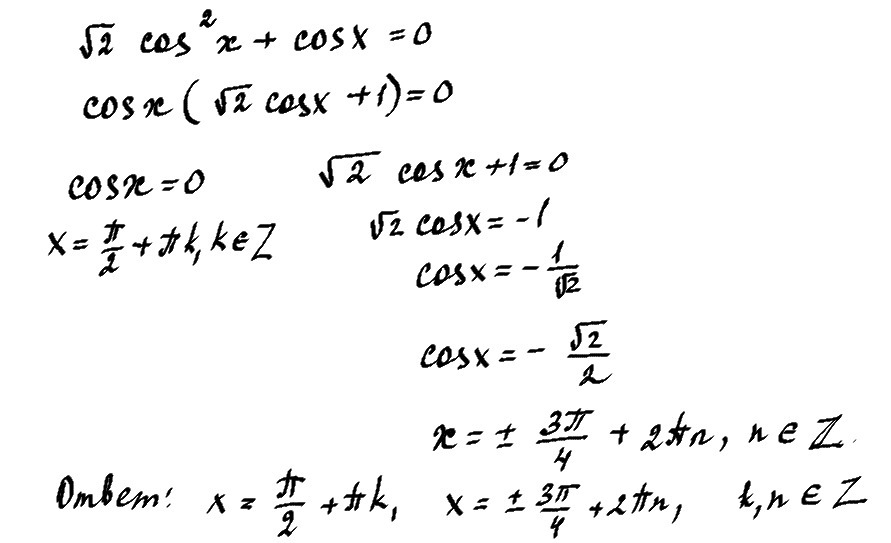
thg20014:
sin^2 x +6 cos^2 x + 7 sin x cos x =0
sin²x+cosx=0 1-cos²x+cosx=0 cos²x-cosx-1=0 пусть cosx=t (|t|<=1) t²-t-1=0 D=5 t=(1+√5)/2 (пост.кор. по ограничению) t=(1-√5)/2 cosx=(1-√5)/2 x=±arccos((1-√5)/2) +2πn n∈Z
sin²x+6cos²x+7sinxcosx=0 sin²x+sinxcosx+6cos²x+6sinxcosx=0 sinx(sinx+cosx)+6cosx(cosx+sinx)=0 (sinx+cosx)(sinx+6cosx)=0
sinx+cosx=0(делим все на cosx, cosx не равно 0, т.к. иначе и sinx=0, что противоречит основному тригонометрическому тождеству)
аналогично sinx+6cosx=0 делим на cosx
tgx=-1 tgx=-6
x=π/4+πn n∈Z
x=-arctg(6)+πk k∈Z
надеюсь все понятно
Спасибо большое
Автор ответа:
2
√2cos²x+cosx=0
cosx(√2cosx+1)=0
cosx=0
cosx=-√2/2
x=π/2+πn n∈Z
x=±3π/4+2πk k∈Z
cosx(√2cosx+1)=0
cosx=0
cosx=-√2/2
x=π/2+πn n∈Z
x=±3π/4+2πk k∈Z
Похожие вопросы
Предмет: Математика,
автор: jaraskuanov542
Предмет: Литература,
автор: gelvererik
Предмет: Алгебра,
автор: 3102422
Предмет: Математика,
автор: акто1