Предмет: Геометрия,
автор: SNPC
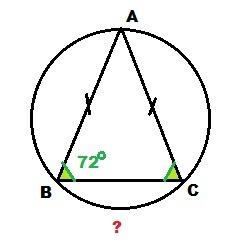
В окружность вписан равнобедренный треугольник A B C с основанием B C . Найдите дугу B C , если ∠ B = 72°.
Ответы
Автор ответа:
2
ΔABC - равнобедренный: AB = AC
∠B = ∠C = 72° (углы при основании BC)
Сумма углов треугольника равна 180° ⇒
∠A = 180° - ∠B - ∠C = 180° - 72° - 72° = 36°
Вписанный угол равен половине дуги, на которую опирается ⇒
Дуга ∪BC = 2*∠A = 2*36° = 72°
Ответ: ∪BC = 72°
∠B = ∠C = 72° (углы при основании BC)
Сумма углов треугольника равна 180° ⇒
∠A = 180° - ∠B - ∠C = 180° - 72° - 72° = 36°
Вписанный угол равен половине дуги, на которую опирается ⇒
Дуга ∪BC = 2*∠A = 2*36° = 72°
Ответ: ∪BC = 72°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: kristinasilnova2004
Предмет: Математика,
автор: aybekraushan
Предмет: Литература,
автор: tarasenkolera052
Предмет: Литература,
автор: shuratolmachev