Question

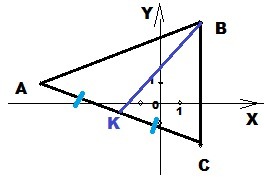
даны координаты вершин треугольника abc a(-6;1) b(2;4) c(2;-2) докажите, что треугольник ABC равнобедренный. Выясните, является ли треугольник ABC прямоугольным. Найдите длинну медианы BK
Как называется тема, зная котррую можно решить эту задачу

Answer 1

1) Чтобы треугольник был равнобедренным, две стороны должны быть равны, то есть расстояния между точками должны быть равными
A(-6;1)   B(2;4)   C(2;-2)
$AB= \sqrt{(X_B-X_A)^2+(Y_B-Y_A)^2}= \\ \\ =\sqrt{(2+6)^2+(4-1)^2} = \sqrt{64+9} =\sqrt{73} \\ \\ AC= \sqrt{(X_C-X_A)^2+(Y_C-Y_A)^2}= \\ \\ =\sqrt{(2+6)^2+(-2-1)^2} = \sqrt{64+9}= \sqrt{73} \\ \\ CB= \sqrt{(X_B-X_C)^2+(Y_B-Y_C)^2}= \\ \\ =\sqrt{(2-2)^2+(4+2)^2} = \sqrt{36} =6$
AB = AC  ⇒ ΔABC - равнобедренный

2) ΔABC :    AB=AC=√73;  BC=6 .
В прямоугольном треугольнике равными могут быть только катеты. Самая длинная сторона - гипотенуза - не может быть равна катетам. 
BC=6 < AB=AC=√73  ⇒  ΔABC не является прямоугольным

3) BK - медиана  ⇒  AK = KC.  Координаты точки K
$X_K= \frac{X_A+X_C}{2} = \frac{-6+2}{2} =-2 \\ \\ Y_K= \frac{Y_A+Y_C}{2} = \frac{1-2}{2} =-0,5$
 B(2;4)   K(-2; -0,5)
$BK = \sqrt{(X_K-X_B)^2+(Y_K-Y_B)^2} = \\ \\ = \sqrt{(-2-2)^2+(-0,5-4)^2}= \sqrt{16+20,25} = \sqrt{36,25}$
BK = √36,25 ≈ 6,02

P.S. Тема: координатная плоскость, координаты точек, расстояние между точками