Предмет: Геометрия,
автор: objebos34p0u005
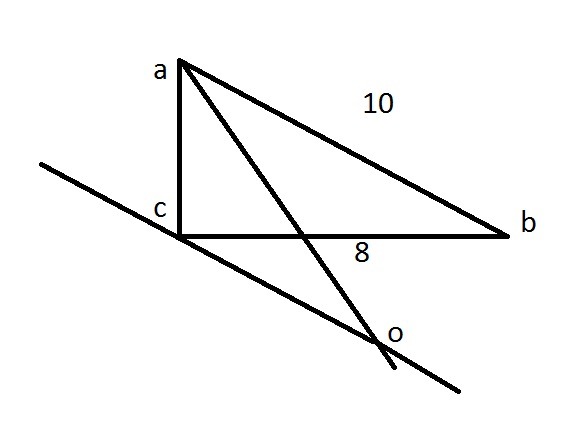
Через вершину прямого угла С треугольника АВС проведена плоскость а ‚ параллельная гипотенузе АВ. Биссектриса угла А треугольника пересекает плоскость а в точке 0. Найдите длину отрезка АО, если АВ = 10, ВС = 8.
Вот примерный рисунок, для удобства:
Варианты ответов:
а) 5 sqrt5
б) 5
в) 4 sqrt6
г) 4.8 sqrt5
д) 6 sqrt5
Приложения:
Ответы
Автор ответа:
2
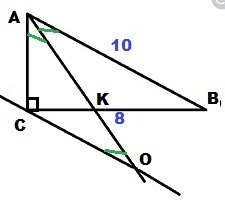
ΔABC - прямоугольный. Теорема Пифагора
AC² = AB² - CB² = 10² - 8² = 36
AC = 6
AK - биссектриса ⇒

KB + KC = BC = 8 ⇒ KB = 5; KC = 3
ΔACK - прямоугольный. Теорема Пифагора
AK² = AC² + KC² = 6² + 3² = 45
AK = √45 = 3√5
AB║CO ⇒ ∠BAO = ∠COA (накрест лежащие углы) ⇒
∠CAO = ∠ COA ⇒ ΔACO - равнобедренный ⇒
CO = AC = 6
ΔAKB ~ ΔOKC по двум равным углам:
вертикальному ∠K и ∠BAK = ∠COK (накрест лежащие)

AO = AK + KO = 3√5 + 1,8√5 = 4,8√5
Ответ: Г) AO = 4,8√5
AC² = AB² - CB² = 10² - 8² = 36
AC = 6
AK - биссектриса ⇒
KB + KC = BC = 8 ⇒ KB = 5; KC = 3
ΔACK - прямоугольный. Теорема Пифагора
AK² = AC² + KC² = 6² + 3² = 45
AK = √45 = 3√5
AB║CO ⇒ ∠BAO = ∠COA (накрест лежащие углы) ⇒
∠CAO = ∠ COA ⇒ ΔACO - равнобедренный ⇒
CO = AC = 6
ΔAKB ~ ΔOKC по двум равным углам:
вертикальному ∠K и ∠BAK = ∠COK (накрест лежащие)
AO = AK + KO = 3√5 + 1,8√5 = 4,8√5
Ответ: Г) AO = 4,8√5
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: География,
автор: dasha83top
Предмет: Алгебра,
автор: kurasovplat277
Предмет: История,
автор: Elza132
Предмет: Литература,
автор: mvasilaki