Предмет: Алгебра,
автор: Аноним
Найдите экстремумы функций
Приложения:
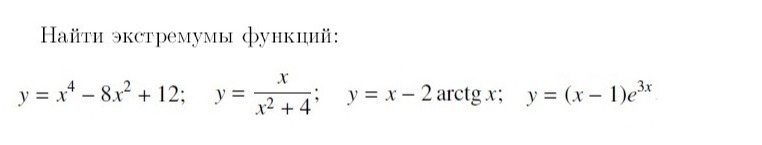
Ответы
Автор ответа:
0
y=x⁴-8x²+12 y'=4x³-16x=0 4x(x²-4x)=0 x1=0 x²=4x x2=4
--------------------- -----------------------------------
y=x/(x²+4) y'=u'v+v'u u=x u'=1 v=x²+4 v'=2x
y'=1/(x²+4)²[x²+4+2x*x] 3x²+4=0 экстр. нет
--------------------------- --------------------------------
y=x-2arctgx y'=1-2/(1+x²) 1=2/(1+x²) 1+x²=2 x²=1 x1=-1 x2=1
----------------------------- -------------------------------------------
y=(x-1)e³ˣ u=x-1 u'=1 v=e³ˣ v'=3e³ˣ
y'=1/(3e³ˣ)²[e³ˣ+(x-1)3e³ˣ ]
e³ˣ+(x-1)3e³ˣ=e³ˣ(1+3x-3)=0
3x=2 x=2/3
--------------------- -----------------------------------
y=x/(x²+4) y'=u'v+v'u u=x u'=1 v=x²+4 v'=2x
y'=1/(x²+4)²[x²+4+2x*x] 3x²+4=0 экстр. нет
--------------------------- --------------------------------
y=x-2arctgx y'=1-2/(1+x²) 1=2/(1+x²) 1+x²=2 x²=1 x1=-1 x2=1
----------------------------- -------------------------------------------
y=(x-1)e³ˣ u=x-1 u'=1 v=e³ˣ v'=3e³ˣ
y'=1/(3e³ˣ)²[e³ˣ+(x-1)3e³ˣ ]
e³ˣ+(x-1)3e³ˣ=e³ˣ(1+3x-3)=0
3x=2 x=2/3
Автор ответа:
1
1) y = x^4-8x^2+12
y' = 4x^3-16x = 4x(x^2-4) = 4x(x-2)(x+2) = 0
x1 = -2; y(-2) = 16-8*4+12 = -4 - минимум.
x2 = 0; y(0) = 12 - максимум.
x3 = 2; y(2) = 16-8*4+12 = -4 - минимум.
2) y = x/(x^2+4) = u/v
y' = (u'*v-u*v')/v^2 = [1*(x^2+4)-x*2x]/(x^2+4)^2 = 0
(4-x^2)/(x^2+4)^2 = (2+x)(2-x)/(x^2+4)^2 = 0
x1 = -2; y(-2) = -2/(4+4) = -1/4 - минимум.
x2 = 2; y(2) = 2/(4+4) = 1/4 - максимум.
3) y = x-2arctg x
y' = 1-2/(1+x^2) = (1+x^2-2)/(1+x^2) = (x^2-1)/(x^2+1) = (x+1)(x-1)/(x^2+1) = 0
x1 = -1; y(-1) = -1-2arctg(-1) = -1+2arctg 1 ~ 0,57 - максимум.
x2 = 1; y(1) = 1-2arctg 1 ~ -0,57 - минимум.
4) y = (x-1)*e^(3x) = u*v
y' = u'*v+u*v' = 1*e^(3x)+3(x-1)*e^(3x) = e^(3x)*(1+3x-3) = 0
e^(3x) > 0 при любом x.
3x -2 = 0
x = 2/3; y(2/3) = (2/3-1)*e^2 = -1/3*e^2 - минимум.
y' = 4x^3-16x = 4x(x^2-4) = 4x(x-2)(x+2) = 0
x1 = -2; y(-2) = 16-8*4+12 = -4 - минимум.
x2 = 0; y(0) = 12 - максимум.
x3 = 2; y(2) = 16-8*4+12 = -4 - минимум.
2) y = x/(x^2+4) = u/v
y' = (u'*v-u*v')/v^2 = [1*(x^2+4)-x*2x]/(x^2+4)^2 = 0
(4-x^2)/(x^2+4)^2 = (2+x)(2-x)/(x^2+4)^2 = 0
x1 = -2; y(-2) = -2/(4+4) = -1/4 - минимум.
x2 = 2; y(2) = 2/(4+4) = 1/4 - максимум.
3) y = x-2arctg x
y' = 1-2/(1+x^2) = (1+x^2-2)/(1+x^2) = (x^2-1)/(x^2+1) = (x+1)(x-1)/(x^2+1) = 0
x1 = -1; y(-1) = -1-2arctg(-1) = -1+2arctg 1 ~ 0,57 - максимум.
x2 = 1; y(1) = 1-2arctg 1 ~ -0,57 - минимум.
4) y = (x-1)*e^(3x) = u*v
y' = u'*v+u*v' = 1*e^(3x)+3(x-1)*e^(3x) = e^(3x)*(1+3x-3) = 0
e^(3x) > 0 при любом x.
3x -2 = 0
x = 2/3; y(2/3) = (2/3-1)*e^2 = -1/3*e^2 - минимум.
Похожие вопросы
Предмет: Математика,
автор: skedg
Предмет: Физика,
автор: polinashmelik2825
Предмет: Математика,
автор: terens19
Предмет: Алгебра,
автор: Лунара41
Предмет: История,
автор: Аноним