Question

Скажите, пожалуйста, это утверждение верно или нет:
Если в треугольник вписана окружность, то площадь его равна произведению полупериметра на радиус вписанной окружности

Answer 1

Верно
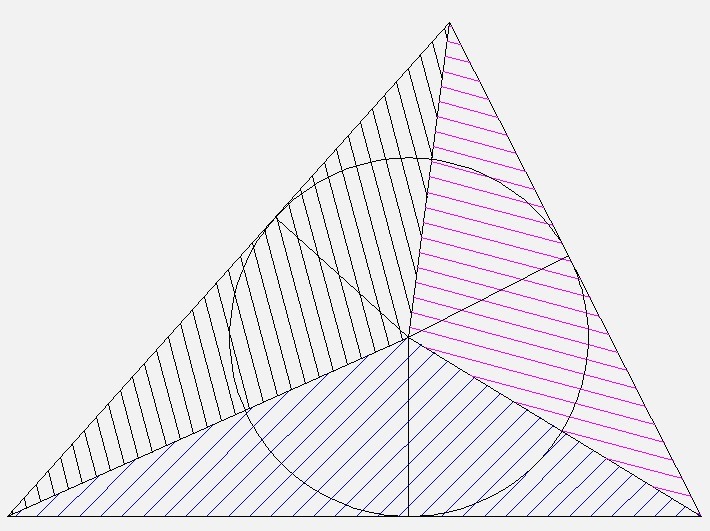
Если исходный треугольник разрезать на три дочерних, то получится, что у всех трёх высота равна радиусу вписанной окружности, площади
S₁ = 1/2*a*r
S₂ = 1/2*b*r
S₃ = 1/2*c*r
S = S₁ + S₂ + S₃ = 1/2*a*r + 1/2*b*r + 1/2*c*r = 1/2(a+b+c)*r 
т.е половина периметра, умноженная на радиус вписанной окружности.