Предмет: Геометрия,
автор: Lolkilita
ПОМОГИТЕ ПОЖАЛУЙСТА ОЧЕНЬ НУЖНО
ГЕОМЕТРИЯ 8 КЛАСС
"В прямоугольном треугольнике АВС (∠C - 90°) BD – биссектриса. Площади треугольников ABD и BCD относятся как 17 : 8. Найдите синус угла АВС."
Аноним:
3/корень из 34
это синус половины угла...
sinABC=30/34
или 15/17
А подробнее можно?
Ответы
Автор ответа:
1
AD/DC=17/8(высоты у треугольников одинаковы)
ВС у ΔАВС И ΔBCD одинаковы, поэтому я все привязала к ВС и углу АВС
tg(<DBC)=DC/CB; tg(<ABC)=AC/CB
<DBC=x; <ABC=2x
DA=17a; CD=8a
подставлю все это
tgx=8a/CB; tg2x=25a/CB
выражу СВ слева и справа и приравняю
8a/tgx=25a/tg2x
tg2x/tgx=25/8
tg2x=2tgx/(1-tg^2x)
tg^2x=9/25; tgx=3/5
1/(sin^2x)=1/tg^2x+1
подставляя все получу sin^2x=9/34
sinx=3/√34
sin2x=2sinx*cosx
cosx нахожу из основного тождества
cosx=5/√34
sin2x=sin(<ABC)=2*3*5/34=30/34=15/17
ВС у ΔАВС И ΔBCD одинаковы, поэтому я все привязала к ВС и углу АВС
tg(<DBC)=DC/CB; tg(<ABC)=AC/CB
<DBC=x; <ABC=2x
DA=17a; CD=8a
подставлю все это
tgx=8a/CB; tg2x=25a/CB
выражу СВ слева и справа и приравняю
8a/tgx=25a/tg2x
tg2x/tgx=25/8
tg2x=2tgx/(1-tg^2x)
tg^2x=9/25; tgx=3/5
1/(sin^2x)=1/tg^2x+1
подставляя все получу sin^2x=9/34
sinx=3/√34
sin2x=2sinx*cosx
cosx нахожу из основного тождества
cosx=5/√34
sin2x=sin(<ABC)=2*3*5/34=30/34=15/17
Приложения:
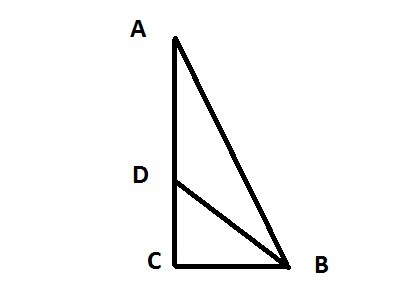
решение длинное, но может есть и короче..
Похожие вопросы
Предмет: Химия,
автор: hatreus666
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Пухлик10