Question

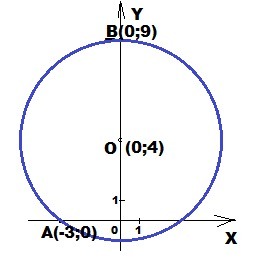
3) Составьте уравнения окружности с центром на оси ординат, которая проходит через точки A(-3;0), B(0;9)

Answer 1

Уравнение окружности имеет вид:
R² = (x - X₀)² + (y - Y₀)²  ,
       где (X₀; Y₀) - центр окружности, R - радиус
Центр окружности на оси ординат  ⇒  координата X₀ = 0
Чтобы найти координату Y₀, нужно уравнять расстояния от точек А(-3;0) и В(0;9) до центра окружности O(0; Y₀)
$R^2 = (x_A-X_0)^2 + (y_A-Y_0)^2=(x_B-X_0)^2+(y_B-Y_0)^2$
(-3 - 0)² + (0 - Y₀)² = (0 - 0)² + (9 - Y₀)²
9 + Y₀² = 81 - 18Y₀ + Y₀²
18Y₀ = 72
Y₀ = 4
Радиус окружности равен
$R^2 = (x_A-X_0)^2 + (y_A-Y_0)^2$=
= (-3 - 0)² + (0 - 4)² = 25

Ответ: x² - (y - 4)² = 25