Предмет: Геометрия,
автор: HNLLZ
Найдите диагонали параллелограмма, построенного на векторах а=5р+2q и b=p-3q, если |р|=2√2, |q|=3(над p и q значки векторов). Угол между векторами р и q равен 45°.
Аноним:
нет
Тут вот 45 известен
да я знаю как их находить-просто смотрю каклучше сделать
Если что ответы 15 и 23,4
хорошо,отдохни пока
класс 9?
вообще меня смущает что длины векторов не целые
вообщем завязла я с этими углами...
сейчас распишу
Да, 9 класс
Ответы
Автор ответа:
5
AC=a+b=5p+2q+p-3q=6p-q
|AC|=√((6p)^2+q^2-2*6p*q*cos45)=√(288+9-2*6*2√2*3*√2/2)=√225=15
BD=b-a=p-3q-5p-2q=-4p-5q
|BD|=√(-4p)^2+(-5q)^2-2(-4p)(-5q)cos45)=√593=23.4 примерно...
|AC|=√((6p)^2+q^2-2*6p*q*cos45)=√(288+9-2*6*2√2*3*√2/2)=√225=15
BD=b-a=p-3q-5p-2q=-4p-5q
|BD|=√(-4p)^2+(-5q)^2-2(-4p)(-5q)cos45)=√593=23.4 примерно...
Приложения:
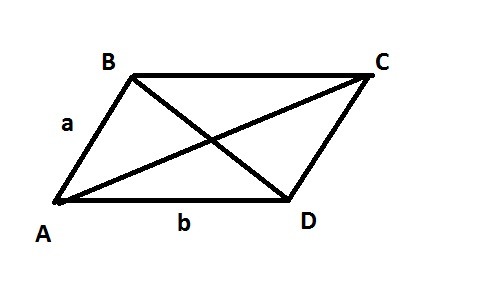
Где |АС|-это теорема косинусов?
да и где BD -то же
Спасибо)
Похожие вопросы
Предмет: История,
автор: koshifialka
Предмет: Информатика,
автор: Аноним
Предмет: Математика,
автор: aaaleeon
Предмет: Математика,
автор: dario4irowa