Предмет: Математика,
автор: robeberhard
Сколько существует целых значений a, для которых неравенство имеет хотя бы одно решение.
Приложения:
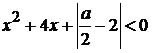
Ответы
Автор ответа:
1
Пусть
Выражение слева обращается в нуль при
Неравенство выполняется при
Т.е. при
Чтобы существовало хотя бы одно решение, нужно чтобы
Объединяем:
Считаем целые а в этом интервале:
-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Проверка показывает, что при а=-4 дискриминант тоже обращается в нуль, а это приводит к тому, что исходное неравенство не выполняется. Поэтому всего 15 целых значений.
Похожие вопросы
Предмет: Литература,
автор: jfjdkflsls
Предмет: История,
автор: taniahoptiy25
Предмет: Другие предметы,
автор: thailandgirl1021
Предмет: Математика,
автор: DS11
Предмет: Математика,
автор: OrlovaNatasha