Question

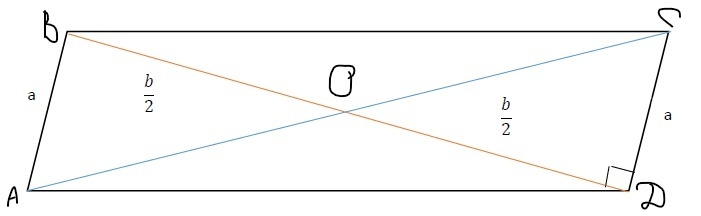
Диагональ параллелограмма, равная b перпендикулярна стороне параллелограмма, равной а. Найдите вторую диагональ параллелограмма.

Answer 1

Как известно, диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. 
OC=0,5AC
Чтобы найти АС, воспользуемся теоремой Пифагора:
$OC^{2}= OD^{2} + CD^{2} \\ OC= \sqrt{OD^{2} + CD^{2}} = \sqrt{ ( \frac{b}{2} )^{2} + a^{2} } = \sqrt{ \frac{ b^{2} }{4} + a^{2} } = \\ = \sqrt{ \frac{ b^{2} + 4a^{2} }{4} }= \frac{ \sqrt{ b^{2} + 4a^{2} } }{2} \\ \\ AC=2OC=2* \frac{ b^{2} + 4a^{2} }{2} = \sqrt{ b^{2}+4a^{2} }$

Ответ: $AC= \sqrt{ b^{2} + 4a^{2} }$