Question

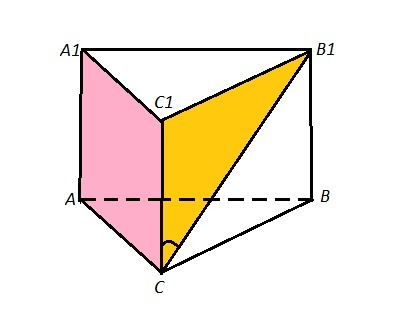
ABCA1B1C1 - прямая призма
треугольник ABC - правильный
AB = 1
BB1 = √2
Надо найти угол (СB1, (AA1C))
Нужен не столько ответ сколько сам ход решения

Answer 1

Угол между СВ1 и пл. АА1С1С - это угол между СВ1 и её проекцией на плоскость АА1С1С.Из точки С опускаем перпендикуляр на пл. АА1С1С. Это будет отрезок В1С1, т.к. призма прямая, то ребро В1С1 перпендикулярно АА1С1С и соответственно В1С1 перпендикулярно СС1 (любой прямой в пл. АА1С1С).СС1 - проекция СВ1 . Тогда искомый угол - это угол С1СВ1. 
СС1=√2 , В1С1=1 
ΔСС1В1:  ∠СС1В1=90° , tg∠C1CB1=B1C1/CC1=1/√2=√2/2  ⇒
   ∠C1CB1=arctg√2/2.
Или:  sin∠C1CB1=B1C1/CB1=1/(√(2+1))=1/√3=√3/3  ⇒
   ∠C1CB1=arcsin√3/3.