Предмет: Геометрия,
автор: cheloveki1
помогите плиз!
даны сторона тругольника а и поижащие ей углы А, Б. найдите их биссектриссы.
желательно с объяснением
Ответы
Автор ответа:
1
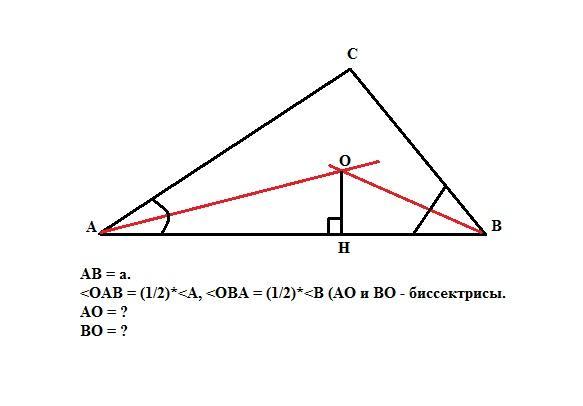
Сторона треугольника АВ = "а". Пусть точка О - точка пересечения биссектрис. Опустим перпендикуляр ОН на сторону АВ. Пусть в прямоугольном треугольнике АОН катет АН = х. Тогда в прямоугольном треугольнике ВОН катет ВН = (а-х). Выразим радиус r вписанной окружности (общий катет треугольников) через второй катет и угол, прилежащий к этому катету. r = x*tg(A/2) и r = (a-x)*tg(B/2). Приравняем оба выражения.
x*tg(A/2) = (a-x)*tg(B/2) => x = a*tg(B/2)/(tg(A/2)+tg(B/2)).
Тогда r = a*tg(B/2)*tg(A/2)/(tg(A/2)+tg(B/2)).
Найдем биссектрисы АО и ВО из треугольников АОН и ВОН:
АО = r/Sin(A/2) = a*tg(A/2)*tg(B/2)/(Sin(A/2)(tg(A/2)+tg(B/2))).
BO = r/Sin(B/2) = a*tg(A/2)*tg(B/2)/(Sin(B/2)(tg(A/2)+tg(B/2))).
Приложения:
Похожие вопросы
Предмет: Химия,
автор: nadia9398
Предмет: Информатика,
автор: crowerey2
Предмет: Математика,
автор: natashakumir
Предмет: Математика,
автор: Безумная111