Question

основа равнобедреннного треугольника равна 12 см. Найдите боковую сторону треугольника, если угол при его вершине равен 120 градусов

Answer 1

В решении задачи используется свойство равнобедренного треугольника: медиана к основанию является биссектрисой и высотой, а также свойство прямоугольного треугольника: катет, лежащий против ушла в 30 градусов, равен половине гипотенузы. Сторона треугольника обозначается за х, высота (медиана, высота) - х/2. Затем составляется уравнение по теореме Пифагора. Решение на листочке.

Answer 2

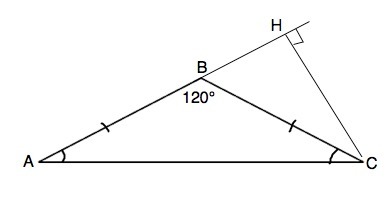
Задачу можно решить несколькими способами. Один из них: 

Т.к. ∆ АВС равнобедренный,∠А=∠С=(180°-угол В):2=(180°-120°):2=30°

Проведем высоту из вершины С треугольника АВС,

Т.к. угол АВС тупой, высота будет расположена вне треугольника и пересечёт продолжение АВ в т.Н.

∆ АНС прямоугольный с острым углом А=30°. Катет СН противолежит углу 30° и равен половине АС. 

СН=12:2=6 см.

Угол НВС смежный углу АВС и равен 180°-120°=60°. ⇒

Боковая сторона ВС=НС:sin60°=6:√3/2=4√3 см

(Тот же результат получится. если применить 

1)т.Пифагора

2)т.косинусов

3)т.синусов.