Предмет: Геометрия,
автор: nastenenka
Докажите что если две наклонные проведенные из данной точки к данной прямой имеют равные проекции то они равны (рис.14.6)
Ответы
Автор ответа:
116
Ответ:
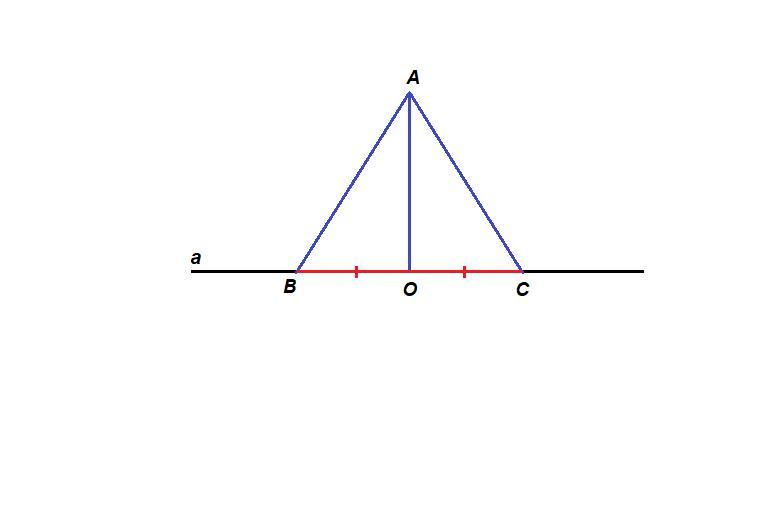
АВ и АС - наклонные к прямой а, АО - перпендикуляр к прямой а.
ОВ и ОС - проекции наклонных.
По условию ОВ = ОС, надо доказать, что АВ = АС.
Рассмотрим ΔАВО и АСО:
∠АОВ = ∠АОС = 90°, так как АО⊥а,
ОВ = ОС по условию,
АО - общий катет, ⇒
ΔАВО = ΔАСО по двум катетам.
Из равенства треугольников следует, что АВ = АС.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: halilovahanumka3
Предмет: Математика,
автор: ariana540
Предмет: История,
автор: xXdoshikXx
Предмет: Химия,
автор: vecherkarina5
Предмет: Математика,
автор: lobe1