Предмет: Алгебра,
автор: BJIADA
Решите неравенство, подробное объяснение
Приложения:
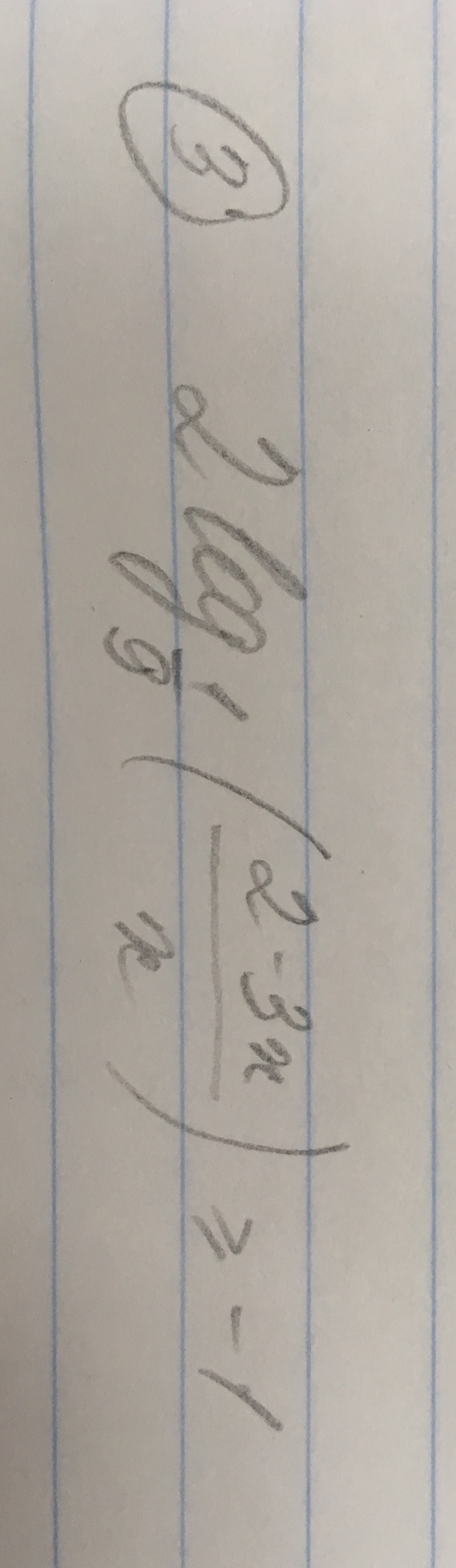
Ответы
Автор ответа:
1
ОДЗ:

x∈(0;2/3)

1/9<1 ⇒ меняем знак

x∈[1/3;+∞)
с учетом ОДЗ, получаем
ОТВЕТ x∈[1/3;2/3)
x∈(0;2/3)
1/9<1 ⇒ меняем знак
x∈[1/3;+∞)
с учетом ОДЗ, получаем
ОТВЕТ x∈[1/3;2/3)
Похожие вопросы
Предмет: География,
автор: iakinkd
Предмет: Математика,
автор: a2021gul
Предмет: Русский язык,
автор: erymbajajko
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Elf1k