Предмет: Алгебра,
автор: BJIADA
Решите неравенство, подробное объяснение
Приложения:
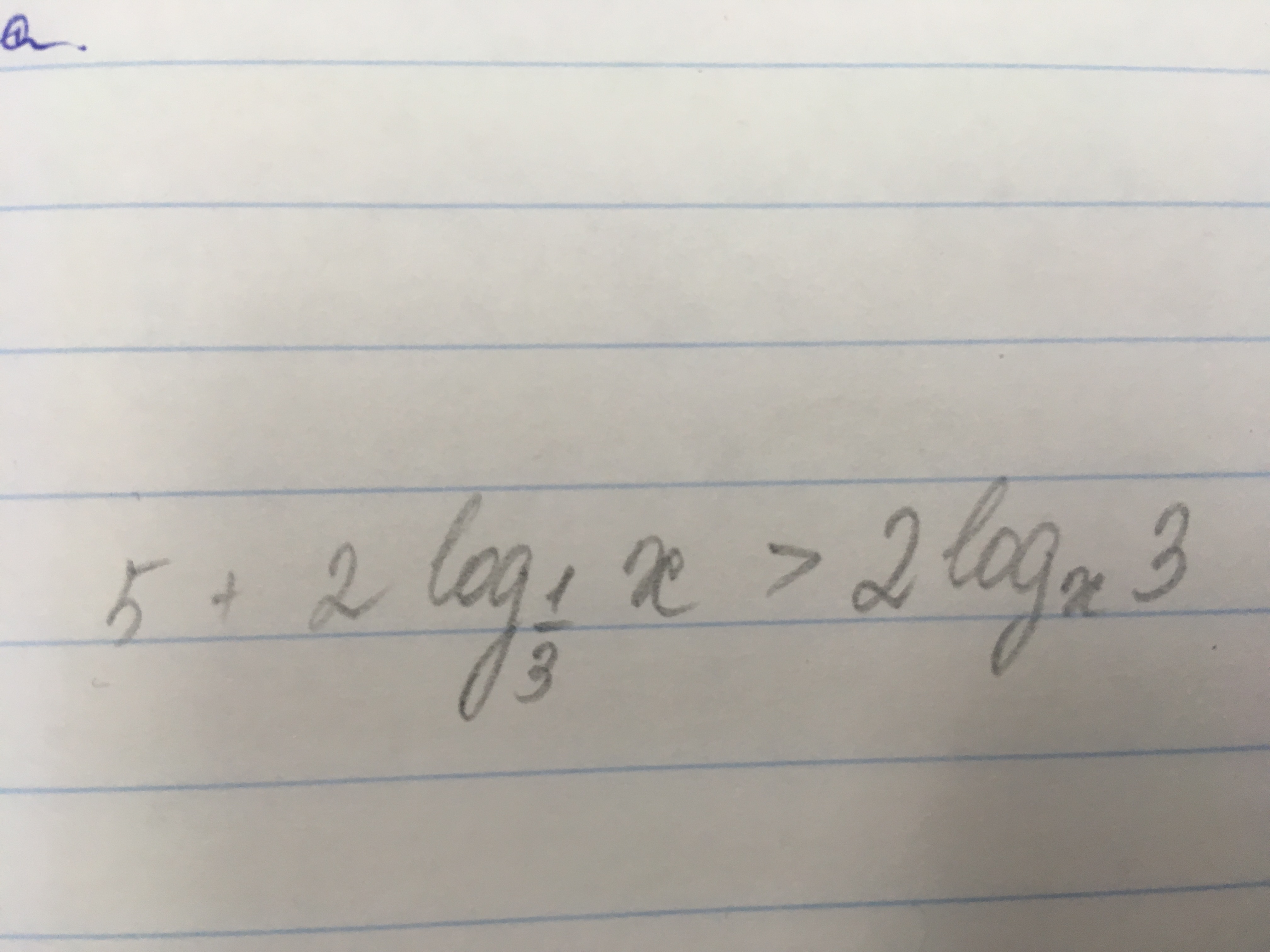
Ответы
Автор ответа:
2
ффффффффффффффффффффффффффффффффффф
Приложения:
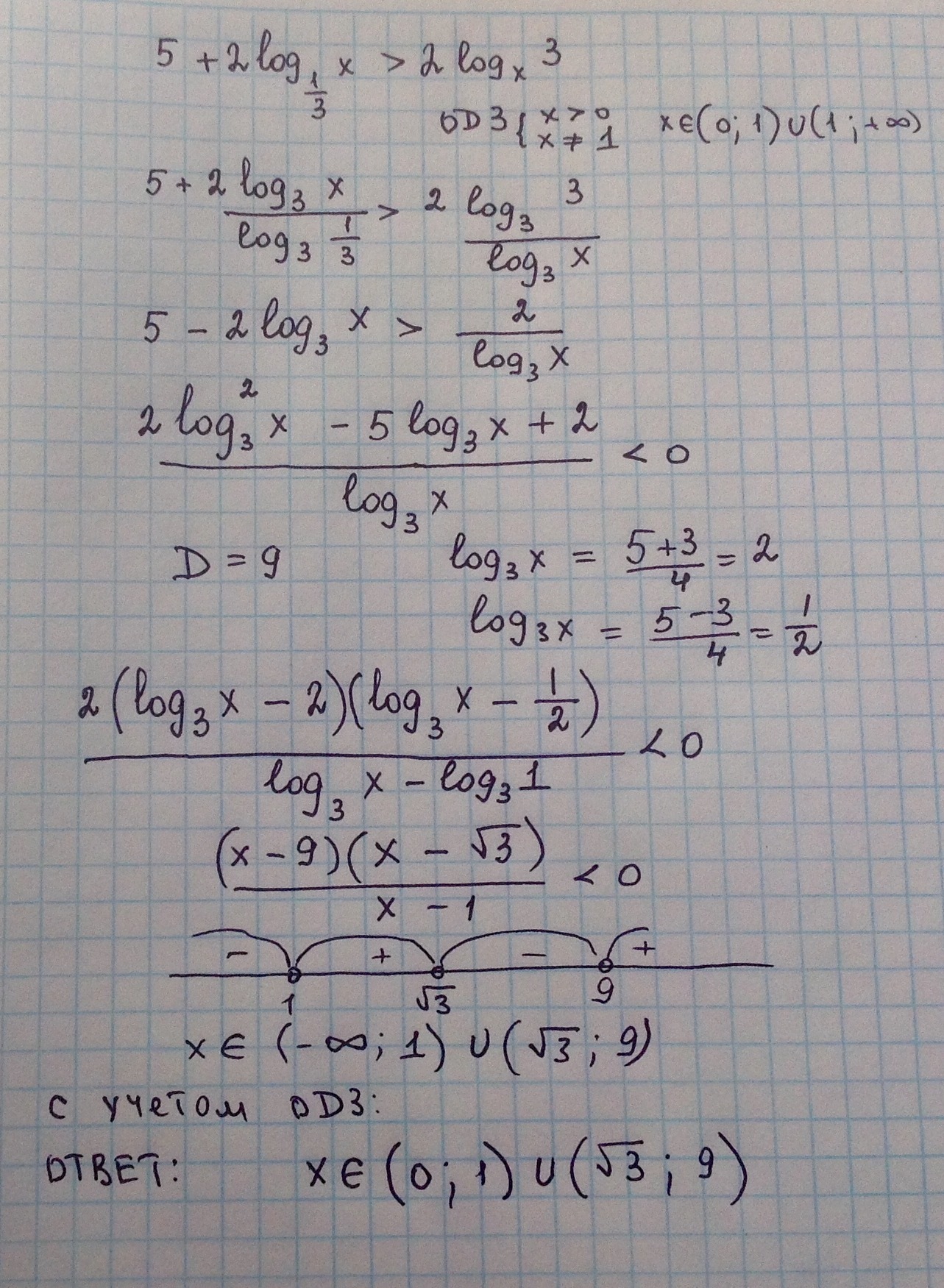
Автор ответа:
0
5+2*log₁/₃ x>2*logₓ3 ОДЗ: x>0 x≠1 ⇒ x∈(0;1)U(1;+∞)
5-2*log₃x>2/log₃x
5-2*log₃x-2/log₃x>0
(5*log₃x-2*log²₃x-2)/log₃x>2
(2*log²₃x-5*log₃x+2)/log₃x<0
2*(log₃x-2)(log₃x-0,5)/log₃x<0 |÷2
(log₃-2)(log₃x-0,5)/log₃x<0
Пусть log₃x=t
(t-2)(t-0,5)/t<0
(t-2)(t-0,5)<0
t>0 log₃x>0 x>1
t₁=2 log₃x=2 x₁=3²=9
t₂=0,5 log₃x=0,5 x₂=√3
-∞______+______√3______-______9______+______+∞
x∈(√3;9)
(t-2)(t-0,5)>0
x∈(-∞;√3)U(9;+∞)
t<0 log₃x<0 x<1
x∈(-∞;1)
Учитывая ОДЗ: x∈(0;1)U(√3;9)
Ответ: x∈(0,1)U(√3;9).
5-2*log₃x>2/log₃x
5-2*log₃x-2/log₃x>0
(5*log₃x-2*log²₃x-2)/log₃x>2
(2*log²₃x-5*log₃x+2)/log₃x<0
2*(log₃x-2)(log₃x-0,5)/log₃x<0 |÷2
(log₃-2)(log₃x-0,5)/log₃x<0
Пусть log₃x=t
(t-2)(t-0,5)/t<0
(t-2)(t-0,5)<0
t>0 log₃x>0 x>1
t₁=2 log₃x=2 x₁=3²=9
t₂=0,5 log₃x=0,5 x₂=√3
-∞______+______√3______-______9______+______+∞
x∈(√3;9)
(t-2)(t-0,5)>0
x∈(-∞;√3)U(9;+∞)
t<0 log₃x<0 x<1
x∈(-∞;1)
Учитывая ОДЗ: x∈(0;1)U(√3;9)
Ответ: x∈(0,1)U(√3;9).
Похожие вопросы
Предмет: Алгебра,
автор: isad21505
Предмет: Геометрия,
автор: mrfroigood
Предмет: Литература,
автор: Lauraersain
Предмет: Алгебра,
автор: Elf1k