Предмет: Алгебра,
автор: bertain
100 баллов. Вычислить интеграл. С подробным (!) объяснением.
Приложения:
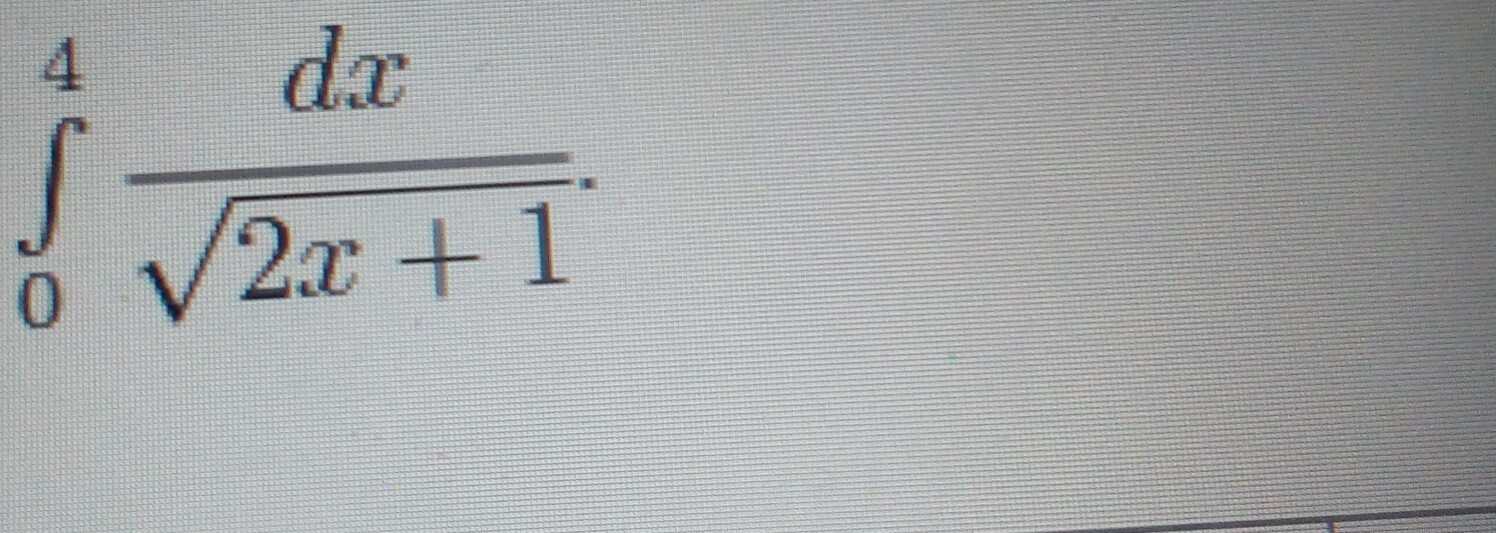
Ответы
Автор ответа:
1
квадратный корень - это степень 1/2, а одно из свойств степени: 1/a^n=a^(-n)

делаем замену:

константа выносится за знак интеграла

Ответ: 2
делаем замену:
константа выносится за знак интеграла
Ответ: 2
bertain:
А можно поподробнее, пожалуйста, этот про переход к данному равенству (2dx=du)? Как именно оно появилось? Никак не могу понять именно этот момент:(
выделение дифферинцала
просто берем производную с обоих сторон и приписываем d
точнее dx
Теперь поняла) Спасибо!
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: bibnjiopfdg
Предмет: Литература,
автор: katrinap2008
Предмет: Литература,
автор: masha2906