Предмет: Алгебра,
автор: sergey831
Пожалуйста помогите решить 5 задание. Я не могу понять как его сделать.
Приложения:
Ответы
Автор ответа:
0
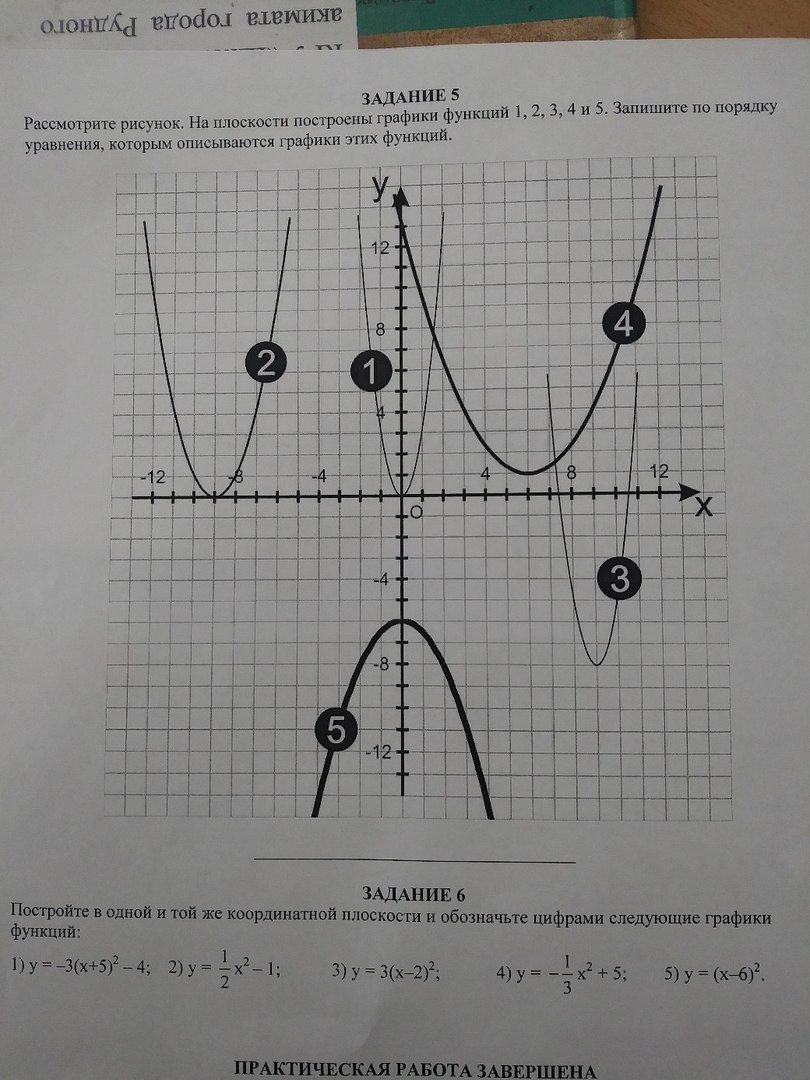
График № 1 y=3x²
График № 2 y=(x+9)²
График № 3 y=3(x-9)²-8
График № 4 y=(4/9)(x-6)²+1
График № 5 y=(-1/2)x²-6
*** Информация к размышлению:
Все графики квадратичной функции получены из базового графика
у=х² путём преобразований - перемещения его по оси Ох, Оу, а также растяжения или сжатия.
Опираемся на уравнение функции
y=k(x-x₀)²+у₀, где x₀- абсцисса вершины параболы,
у₀ - ордината вершины параболы
k - коэффициент растяжения/сжатия при х²
1) Парабола под №1
вершина х₀=0, y₀=0, k=3 (сжатие втрое отн. оси Оу):
Коэфициент k рассчитываем из базового уравнения параболы
y=kx²,подставляя в уравнение удобную нам точку графика
В данном случае, точку (1;3)
3=k*1² => k=3
Получаем уравнение: y=3(x-0)²+0
y=3x²
2) Парабола № 2
x₀=-9, y₀=0,k=1
данная парабола получена из параболы у=х² путём параллельного переноса по оси Ох на 9 единиц влево
у=(х+9)²
3) Парабола № 3
x₀=9, y₀=-8, k=3
данная парабола получена из параболы у=х² путём параллельного переноса по оси Ох на 9 единиц вправо и переноса на 8 единиц вних по оси Оу
у=3(х-9)²-8
4) Парабола № 4
x₀=6, y₀=1, k=4/9
данная парабола получена из параболы у=х² путём параллельного переноса по оси Ох на 6 единиц вправо и переноса на 1 единицу вверх по оси Оу
Точка (3;4) соответствовала бы базовой ф-ции у=х²
y=kx²
4=k*3²
k=4/9
у=4/9(х-6)²+1
5) Парабола № 5
x₀=0, y₀=-6, k=-1/2
данная парабола получена из параболы у=х² путём симметрии относительно оси Ох и параллельного переноса по оси Оу на 6 единиц вниз, а также, растяжения вдвое относительно оси Оу.
Точка (2;-2) соответствовала бы базовой ф-ции у=-х²
y=kx²
-2=k*2²
k=-2/4
у=-1/2x²-6
График № 2 y=(x+9)²
График № 3 y=3(x-9)²-8
График № 4 y=(4/9)(x-6)²+1
График № 5 y=(-1/2)x²-6
*** Информация к размышлению:
Все графики квадратичной функции получены из базового графика
у=х² путём преобразований - перемещения его по оси Ох, Оу, а также растяжения или сжатия.
Опираемся на уравнение функции
y=k(x-x₀)²+у₀, где x₀- абсцисса вершины параболы,
у₀ - ордината вершины параболы
k - коэффициент растяжения/сжатия при х²
1) Парабола под №1
вершина х₀=0, y₀=0, k=3 (сжатие втрое отн. оси Оу):
Коэфициент k рассчитываем из базового уравнения параболы
y=kx²,подставляя в уравнение удобную нам точку графика
В данном случае, точку (1;3)
3=k*1² => k=3
Получаем уравнение: y=3(x-0)²+0
y=3x²
2) Парабола № 2
x₀=-9, y₀=0,k=1
данная парабола получена из параболы у=х² путём параллельного переноса по оси Ох на 9 единиц влево
у=(х+9)²
3) Парабола № 3
x₀=9, y₀=-8, k=3
данная парабола получена из параболы у=х² путём параллельного переноса по оси Ох на 9 единиц вправо и переноса на 8 единиц вних по оси Оу
у=3(х-9)²-8
4) Парабола № 4
x₀=6, y₀=1, k=4/9
данная парабола получена из параболы у=х² путём параллельного переноса по оси Ох на 6 единиц вправо и переноса на 1 единицу вверх по оси Оу
Точка (3;4) соответствовала бы базовой ф-ции у=х²
y=kx²
4=k*3²
k=4/9
у=4/9(х-6)²+1
5) Парабола № 5
x₀=0, y₀=-6, k=-1/2
данная парабола получена из параболы у=х² путём симметрии относительно оси Ох и параллельного переноса по оси Оу на 6 единиц вниз, а также, растяжения вдвое относительно оси Оу.
Точка (2;-2) соответствовала бы базовой ф-ции у=-х²
y=kx²
-2=k*2²
k=-2/4
у=-1/2x²-6
Похожие вопросы
Предмет: Информатика,
автор: ruslanbrob
Предмет: Геометрия,
автор: aluatasenova
Предмет: Українська мова,
автор: orehovaangelina740
Предмет: География,
автор: даяна49