Предмет: Алгебра,
автор: salat1002
Задание 1-5. Заранее спасибо.
Приложения:
Ответы
Автор ответа:
1
task/27896296
-------------------
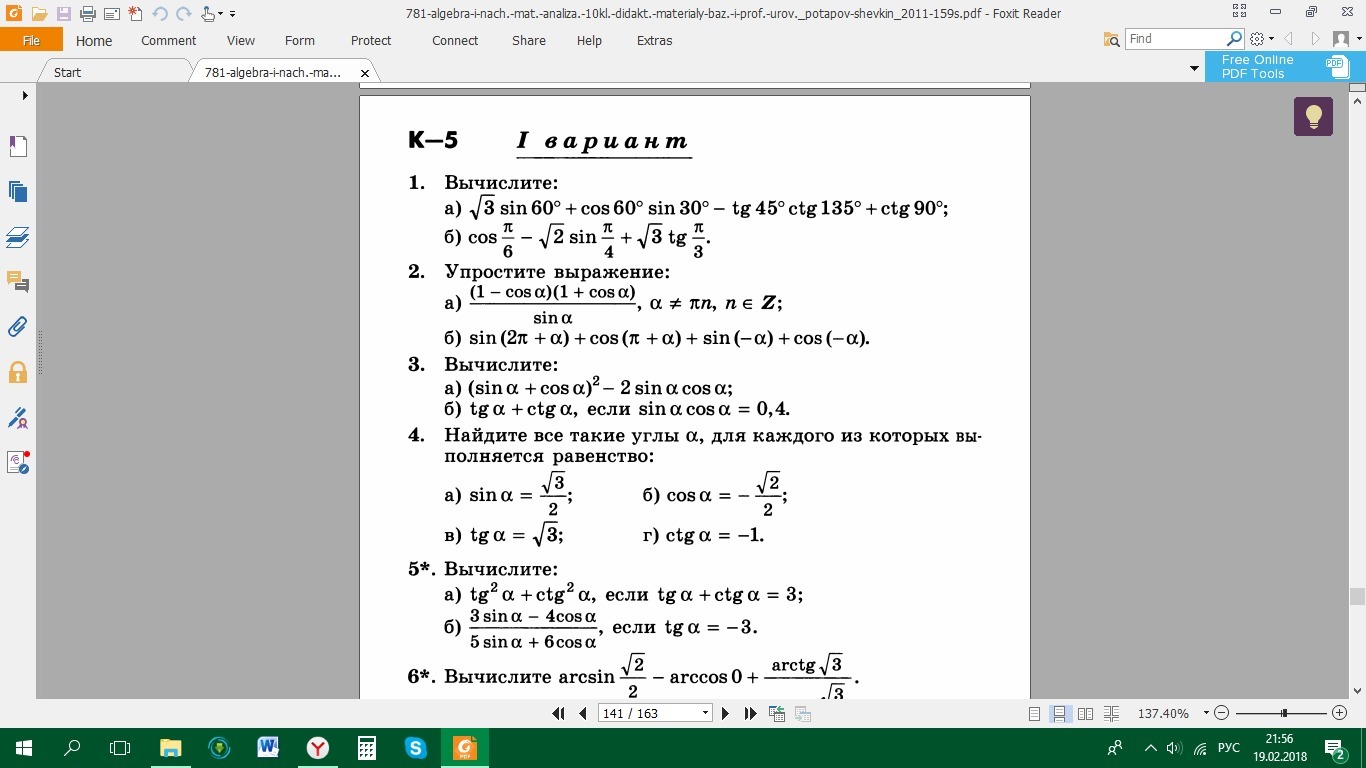
1.Вычислить:
а)
√3sin60°+cos60°sin30°- tg45°ctg135°+ctg90° =
√3*(√3) /2 +(1/2)*(1/2) -1*(-1) +0=3/2 +1/4 +1 =2,75.
---
б)
cos(π/6) -√2sin(π/4) +√3tg(π/3) = (√3)/2 - √2* 1/√2 +√3*√3 = 2 -(√3)/2 .
--------------
2.Упростить выражение :
а)
(1 -cosα)*(1+cosα) /sinα , α≠πn ,n ∈Z.
---
α ≠ πn ,n ∈Z ⇒ sinα ≠0 .
(1 -cosα)*(1+cosα) /sinα =(1-cos²α)/sinα=sin²α /sinα = sinα .
---
б)
sin(2π+α) +cos(π+α)+sin(-α)+cos(-α) =sinα- cosα -sinα +cosα =0.
--------------
3.Вычислить:
а)
(sinα+cosα)² -2sinαcosα=sin²α +2sinαcosα+cos²α - 2sinαcosα =
sin²α +cos²α =1.
---
б)
tgα+ctgα , если sinα*cosα=0,4.
---
tgα+ctgα =sinα/cosα+cosα/sinα = (sin²α+cos²α) / sinα*cosα =1/ 0,4 =2,5.
--------------
4. Найти все такие углы α , для каждого из которых выполняется равенство :
а)
sinα =(√3)/2.
---
α =(-1)ⁿ π/3 +πn , n∈Z.
---
б)
cosα = -(√2)/2 .
---
α =±(π- π/4) +2πn , n∈Z. ⇔ α =±3π/4 +2πn , n∈Z.
в)
tgα=√3 .
---
α = π/3 + πn , n∈Z.
г)
ctgα= -1 .
---
α = - π/4 + πn , n∈Z.
--------------
5. Вычислить:
а)
tg²α+ctg²α , если tgα+ctgα=3.
---
tg²α+ctg²α=(tgα+ctgα)² - 2tgα*ctgα =3² -2*1 =9 -2 =7.
б)
(3sinα - 4cosα) /(5sinα+6cosα) ,если tgα= -3.
---
(3sinα - 4cosα) /(5sinα+6cosα) =(3tgα - 4) /(5tgα+6) =
(3*(-3) - 4)/(5*(-3)+6)= (-13)/ (-9) =13/9 . * * * 1 4/9 * * *
* * * * * * *
Удачи !
-------------------
1.Вычислить:
а)
√3sin60°+cos60°sin30°- tg45°ctg135°+ctg90° =
√3*(√3) /2 +(1/2)*(1/2) -1*(-1) +0=3/2 +1/4 +1 =2,75.
---
б)
cos(π/6) -√2sin(π/4) +√3tg(π/3) = (√3)/2 - √2* 1/√2 +√3*√3 = 2 -(√3)/2 .
--------------
2.Упростить выражение :
а)
(1 -cosα)*(1+cosα) /sinα , α≠πn ,n ∈Z.
---
α ≠ πn ,n ∈Z ⇒ sinα ≠0 .
(1 -cosα)*(1+cosα) /sinα =(1-cos²α)/sinα=sin²α /sinα = sinα .
---
б)
sin(2π+α) +cos(π+α)+sin(-α)+cos(-α) =sinα- cosα -sinα +cosα =0.
--------------
3.Вычислить:
а)
(sinα+cosα)² -2sinαcosα=sin²α +2sinαcosα+cos²α - 2sinαcosα =
sin²α +cos²α =1.
---
б)
tgα+ctgα , если sinα*cosα=0,4.
---
tgα+ctgα =sinα/cosα+cosα/sinα = (sin²α+cos²α) / sinα*cosα =1/ 0,4 =2,5.
--------------
4. Найти все такие углы α , для каждого из которых выполняется равенство :
а)
sinα =(√3)/2.
---
α =(-1)ⁿ π/3 +πn , n∈Z.
---
б)
cosα = -(√2)/2 .
---
α =±(π- π/4) +2πn , n∈Z. ⇔ α =±3π/4 +2πn , n∈Z.
в)
tgα=√3 .
---
α = π/3 + πn , n∈Z.
г)
ctgα= -1 .
---
α = - π/4 + πn , n∈Z.
--------------
5. Вычислить:
а)
tg²α+ctg²α , если tgα+ctgα=3.
---
tg²α+ctg²α=(tgα+ctgα)² - 2tgα*ctgα =3² -2*1 =9 -2 =7.
б)
(3sinα - 4cosα) /(5sinα+6cosα) ,если tgα= -3.
---
(3sinα - 4cosα) /(5sinα+6cosα) =(3tgα - 4) /(5tgα+6) =
(3*(-3) - 4)/(5*(-3)+6)= (-13)/ (-9) =13/9 . * * * 1 4/9 * * *
* * * * * * *
Удачи !
Похожие вопросы
Предмет: Математика,
автор: zhumatsezim
Предмет: Литература,
автор: ek2241632
Предмет: Химия,
автор: muhammadrahimov784
Предмет: Математика,
автор: gravityvod
Предмет: Биология,
автор: Wer222333