Предмет: Математика,
автор: olenkaOO
найти неопределённый интеграл
Приложения:
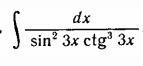
Ответы
Автор ответа:
0
Выполним некоторые преобразования:

А сейчас будет магия. Мы засунем sin3x под d и выполним замену переменной. Имеем право на это, так как
Итак,

А сейчас будет магия. Мы засунем sin3x под d и выполним замену переменной. Имеем право на это, так как
Итак,
Похожие вопросы
Предмет: Биология,
автор: kovdeter
Предмет: Другие предметы,
автор: lucifersatanovic666
Предмет: Информатика,
автор: tojsaidov40
Предмет: Математика,
автор: Аноним