Question

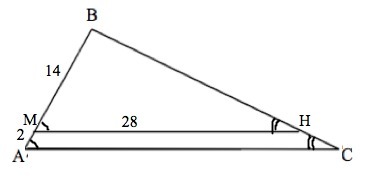
Прямая, параллельная стороне AC треугольника ABC, Пересекает стороны AB и BC Соответственно в точках M и H. Найдите AC и отношение площадей треугольников ABC и BMH, если MB=14см, AM =2см, MH=28см

Answer 1

МН║АС⇒ соответственные углы при пересечении этих прямых секущими АВ и ВС равны. 
Треугольники МВН и АВС подобны по равным углам. 
Из подобия следует отношение: $\frac{MH}{AC}= \frac{MB}{AB}$
 АВ=МВ+АМ=16 см
$\frac{28}{AC}= \frac{14}{16}$⇒
7АС=28•8
АС=4•8=32 см 
Отношение площадей подобных фигур равно квадрату коэффициента их подобия. 
$\frac{S(MBH)}{S(ABC)}=k^2=( \frac{7}{8} )^2= \frac{49}{64}$