Question

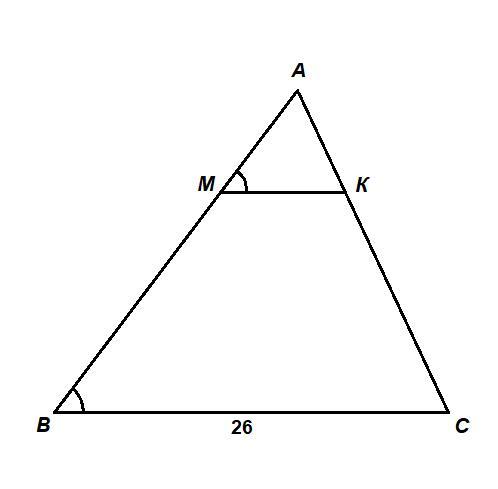
На стороне АВ треугольника АВС отметили точку M так, что АM:MB=4:9. Через точку M провели прямую, которую параллельна стороне BС треугольника и пересекает сторону AС в точке K. Найдите отрезок MK,если BC=26 см.

Answer 1

Ответ:

8 см

Объяснение:

∠АМК = ∠АВС как соответственные при пересечении параллельных прямых МК и ВС секущей АВ,

∠А - общий для треугольников АМК и АВС, значит,

ΔАМК ~ ΔАВС по двум углам.

$\dfrac{MK}{BC}=\dfrac{AM}{AB}$

По условию АМ : МВ = 4 : 9, значит, АМ составляет 4 части, а МВ - 9 таких же частей. Значит, АВ составляет 13 частей. Тогда

$\dfrac{MK}{BC}=\dfrac{AM}{AB}=\dfrac{4}{13}$

$MK=\dfrac{4\cdot BC}{13}=\dfrac{4\cdot 26}{13}=\boldsymbol{8}$ см