Предмет: Алгебра,
автор: SafinaSofiya
СРОЧНО!!ДАМ 80 БАЛЛОВ
Решите систему уравнений
Приложения:
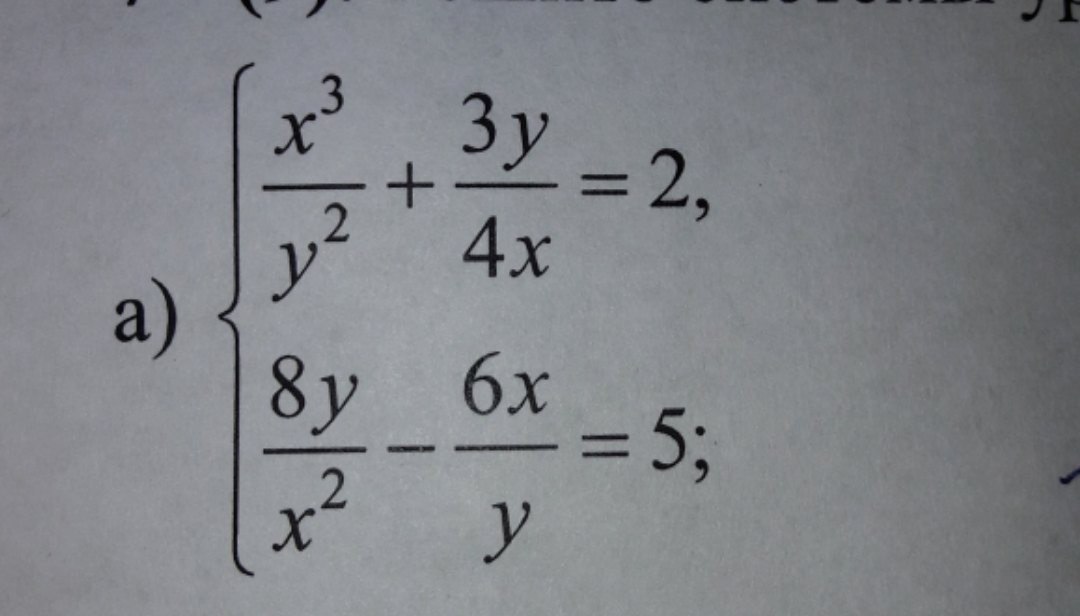
Ответы
Автор ответа:
0
x≠0 y≠0
x₁=(-22y-38y)/32=-15y/8
x₂=(-22+38y)/32=y/2
1) x=-15y/8
подставляем во 2 уравнение
2) x=y/2
ОТВЕТ:
Похожие вопросы
Предмет: Английский язык,
автор: amonovasadcon
Предмет: Русский язык,
автор: Dashik4419
Предмет: Қазақ тiлi,
автор: ajsuzinatova4
Предмет: Математика,
автор: сат12514
Предмет: География,
автор: Лилиана24