Квадрат и прямоугольник, площади которых соответственно равны 36 см² и
54 см², имеют общую сторону, а угол между их плоскостями равен 30 °. Найти расстояние между параллельными сторонами прямоугольника и квадрата.
Квадрат і прямокутник, площі яких відповідно дорівнюють 36 см2 і
54 см2, мають спільну сторону, а кут між їх площинами дорівнює 30°. Знайти відстань між паралельними сторонами прямокутника і квадрата
Ответы
Ответ: ≈14,51 см
Пошаговое объяснение: Угол между плоскостями – двугранный угол. Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.
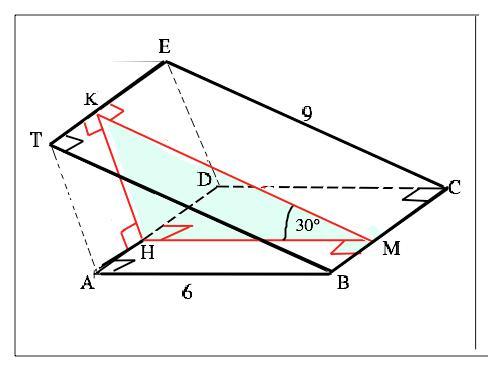
Обозначим квадрат АВСD, прямоугольник ТВСЕ. Ребром угла между их плоскостями является их общая сторона ВС.
КМ⊥ВС, МН⊥ВС. Плоскость, содержащая угол 30°, перпендикулярна плоскостям обеих граней.
АD║ВС, ТЕ║ВС ⇒ ТЕ║AD. Искомое расстояние - длина отрезка КН между ними.
Длина общей стороны ВС данных фигур - сторона квадрата, поэтому ВС=√S=√36=6 см. НМ=АВ=6 см, КМ=ТВ=9 см. т.к. параллельны им и пересекаются с противоположными сторонами прямоугольников под прямым углом.
По т.косинусов КН²=КМ²+НМ*-2КМ•НМ•cos30°
КН²=36+81-2•6•9•√3/2, откуда КН=√(117-54√3)=≈14,51 см