Предмет: Математика,
автор: Мучитель000000
Помогите пожалуйста решить интеграл,задание на фотке.
Приложения:
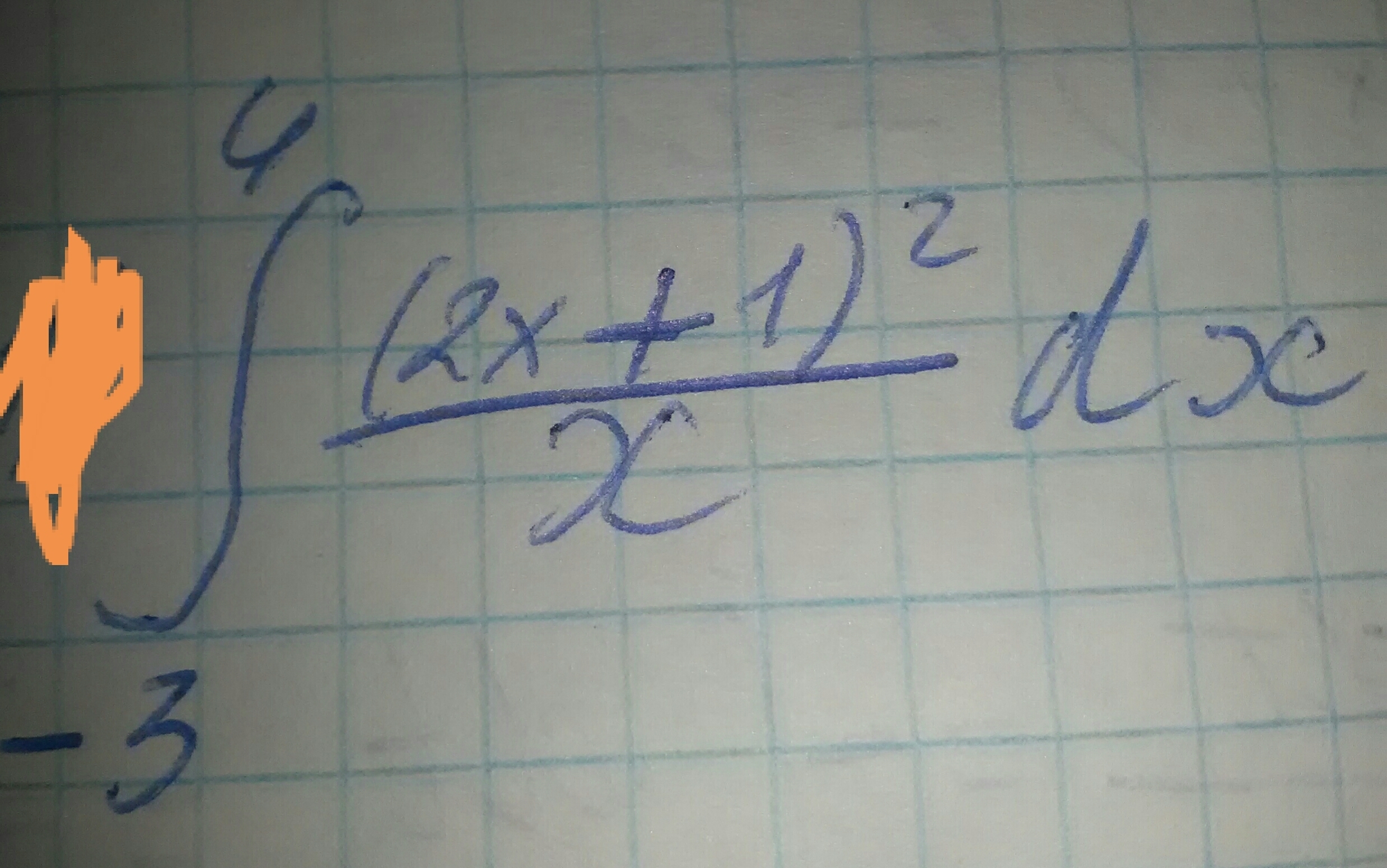
Ответы
Автор ответа:
1
Если нет ошибки в нижнем пределе, и там действительно минус три, то подынтегральная функция в точке х=0 терпит разрыв. Тогда этот интеграл несобственный. Раз уж так получилось, что точка разрыва где-то посередине отрезка интегрирования, то разобьём интеграл на сумму двух:
Интегралы одинаковые, только пределы разные, поэтому для начала возьмём неопределённый интеграл:
А тут ещё одна неприятность вылезла. Если мы будем подставлять в первообразную пределы интегрирования, то столкнёмся с логарифмом от нуля. А логарифм при стремлении переменной к нулю стремится к минус бесконечности!
Значит, несобственный интеграл второго рода расходится.
Похожие вопросы
Предмет: Математика,
автор: maskaevkirill283
Предмет: Математика,
автор: inzhutalgat2011
Предмет: Математика,
автор: maskaevkirill283
Предмет: Математика,
автор: НеизвестныйЧеловечин
Предмет: Алгебра,
автор: FostRine