Предмет: Алгебра,
автор: kata7625
доказать что 9^n+4^n+1: 5
Ответы
Автор ответа:
4
Метод математической индукции
Приложения:
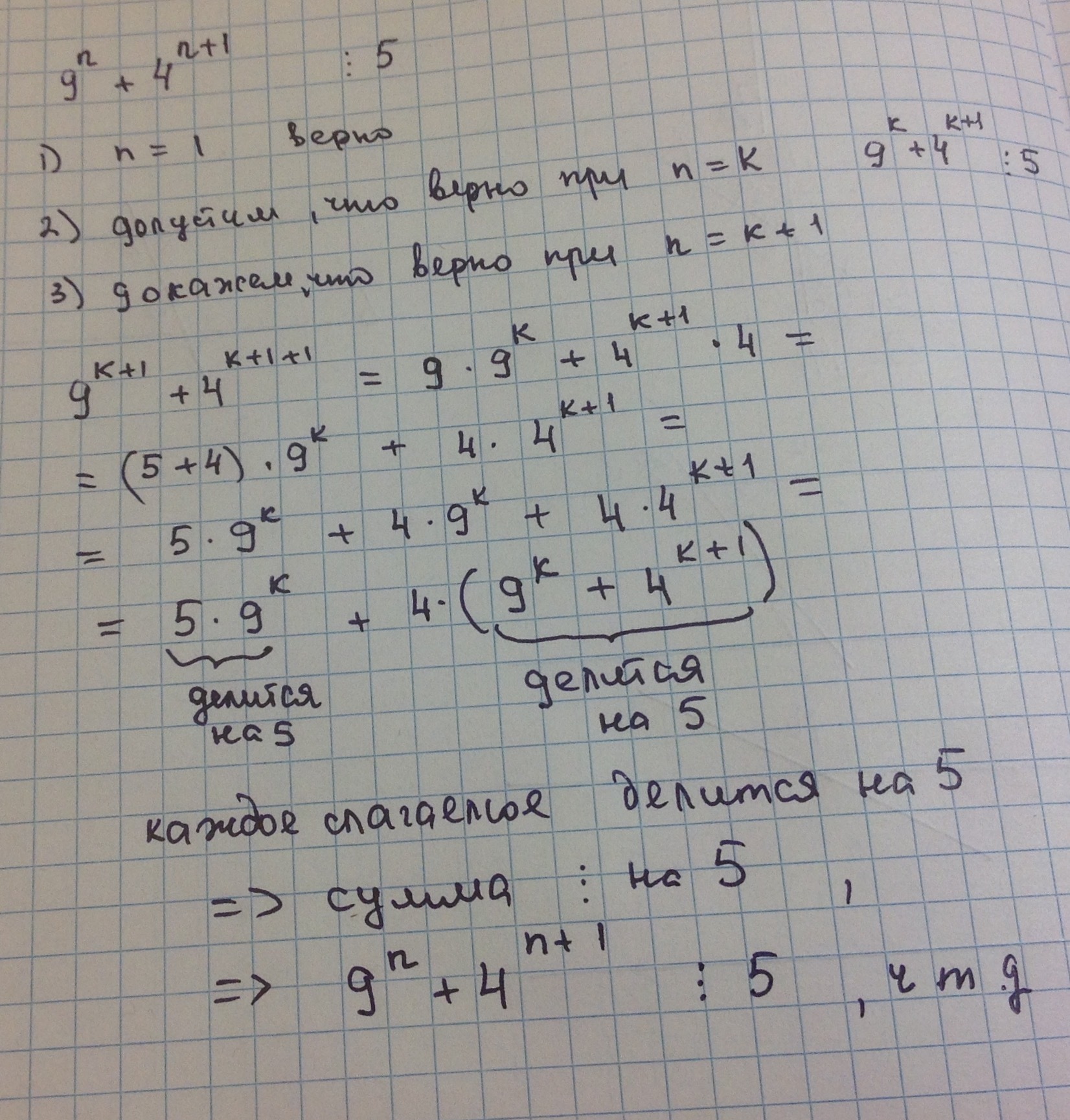
kata7625:
А по другому можно решить?
я просто в 8
Мы такое еще не проходили
Автор ответа:
1
конечно метод математической индукции самый верный способ, но если не проходили, то пойдем другим путем
Признак деления на 5 - когда число оканчивается на 0 или 5
Рассмотрим как что оканчивается каждое слагаемое и сумма, в зависимости от числа
n=1
9^1 = 9 оканчивается на 9
4^2=16 оканчивется на 6
9+6=15 сумма оканчивается на 5
значит сумма делится на 5
n=2
9^2=81 оканчивается на 1
4^3=64 оканчивается на 4
1+4=5 оканчивается на 5
значит сумма делится на 5
n=1
9^3 = 729
4^3=256 на 6
9+6=15 сумма оканчивается на 5
значит сумма делится на 5
n=4
9^4=6561 оканчивается на 1
4^5=1024 оканчивается на 4
1+4=5 оканчивается на 5
значит сумма делится на 5
и так далее
замечаем что
при нечетных n 9^n оканчивается на 9 4^(n+1) оканчивается на 6 сумма заканчивается на 5 и значит число делится на 5
при четных n 9^n оканчивается на 1 4^(n+1) оканчивается на 4 сумма заканчивается на 5 и значит число делится на 5
Таких образом каким бы не была натуральная степень n число всегда делится на 5 так как заканчивается на 5
Признак деления на 5 - когда число оканчивается на 0 или 5
Рассмотрим как что оканчивается каждое слагаемое и сумма, в зависимости от числа
n=1
9^1 = 9 оканчивается на 9
4^2=16 оканчивется на 6
9+6=15 сумма оканчивается на 5
значит сумма делится на 5
n=2
9^2=81 оканчивается на 1
4^3=64 оканчивается на 4
1+4=5 оканчивается на 5
значит сумма делится на 5
n=1
9^3 = 729
4^3=256 на 6
9+6=15 сумма оканчивается на 5
значит сумма делится на 5
n=4
9^4=6561 оканчивается на 1
4^5=1024 оканчивается на 4
1+4=5 оканчивается на 5
значит сумма делится на 5
и так далее
замечаем что
при нечетных n 9^n оканчивается на 9 4^(n+1) оканчивается на 6 сумма заканчивается на 5 и значит число делится на 5
при четных n 9^n оканчивается на 1 4^(n+1) оканчивается на 4 сумма заканчивается на 5 и значит число делится на 5
Таких образом каким бы не была натуральная степень n число всегда делится на 5 так как заканчивается на 5
Похожие вопросы
Предмет: История,
автор: donindima1
Предмет: История,
автор: Аноним
Предмет: Физика,
автор: almatovaksultan66666
Предмет: Математика,
автор: Bella12345678
Предмет: Литература,
автор: Аноним