Question

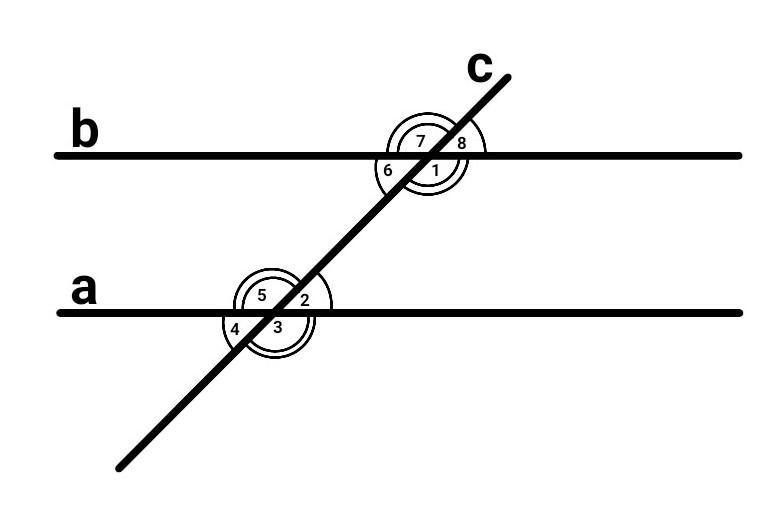
две параллельные прямые пересечены секущей. один из восьми образовавшихся углов равен 129 градусам. найдите остальные углы

Answer 1

Две параллельные прямые пересечены секущей. Один из восьми образовавшихся углов равен 129 градусам. Найдите остальные углы.

Пусть ∠1 = 129°

∠1 + ∠2 = 180° (сумма смежных углов)

Тогда:

∠2 = 180 - ∠1 = 180 - 129 = 51°

∠2 = ∠6 = 51° (как соответственные при параллельных прямых)

∠6 = ∠3 = 51° (как накрест лежащие при параллельных прямых)

∠3 = ∠7 = 51° (как соответственные при параллельных прямых)

∠1 = ∠5 = 129° (как соответственные при параллельных прямых)

∠5 = ∠4 = 129° (как накрест лежащие при параллельных прямых)

∠4 = ∠8 = 129° (как соответственные при параллельных прямых)

Ответ: ∠1, ∠5, ∠4, ∠8 = 129°; ∠2, ∠3, ∠6, ∠7 = 51°

Answer 2

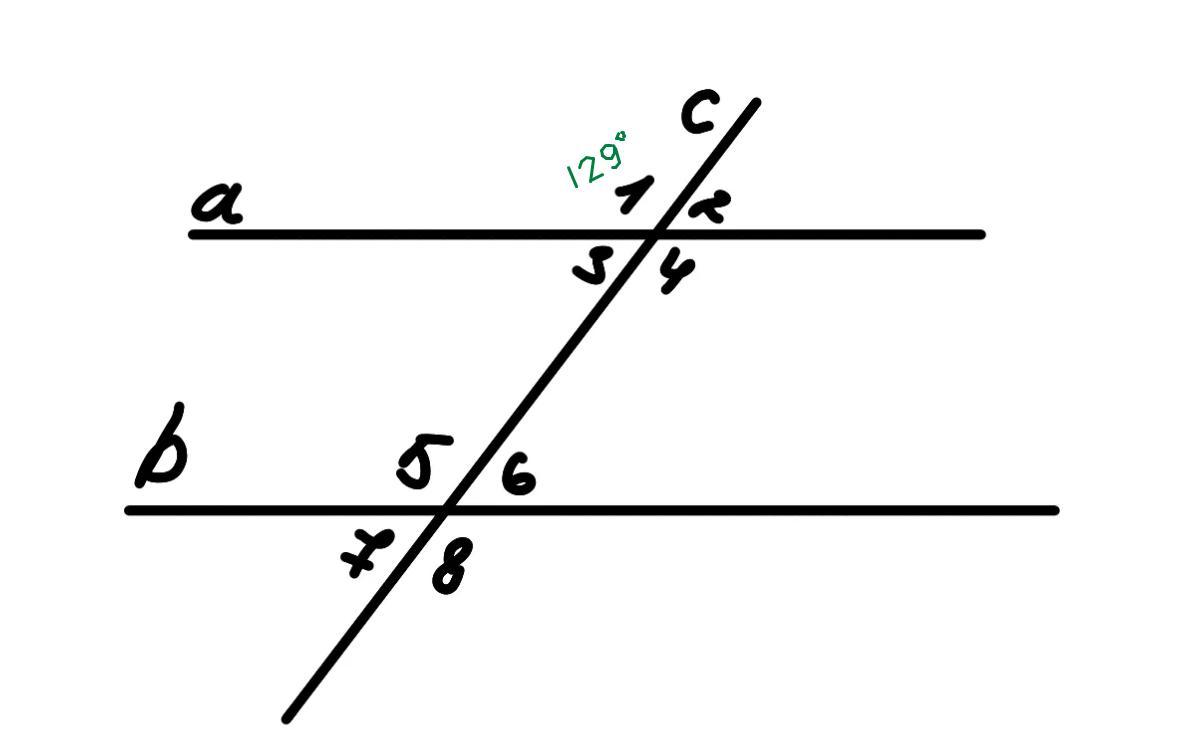
Дано :

a || b.

c - секущая.

<1 = 129°.

Найти :

<2 = ?

<3 = ?

<4 = ?

<5 = ?

<6 = ?

<7 = ?

<8 = ?

Решение :

• При пересечении двух параллельных прямых секущей накрест лежащие углы равны, соответственные углы равны, сумма односторонних углов равна 180°.

<1 и <2 — односторонние.

По выше сказанному —

<1 + <2 = 180°

<2 = 180° - <1 = 180° - 129° = 51°.

<2 = <6 = 51° — как накрест лежащие при параллельных прямых

<1 = <3 = 129° — как соответственные при параллельных прямых

<2 = <8 = 51° — как соответственные при параллельных прямых

<2 = <4 = 51° — как вертикальные

<1 = <7 = 129° — как вертикальные

<1 = <5 = 129° — как накрест лежащие при параллельных прямых

Ответ :

51°, 129°, 51°, 129°, 51°, 129°, 51°.