Предмет: Алгебра,
автор: DOandDO
Докажите следующее равенство
Приложения:
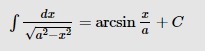
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: sedojkinaevgenia
Предмет: История,
автор: ogonek666666
Предмет: Музыка,
автор: annachornomorets60
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: annna6