Предмет: Геометрия,
автор: mionkaf1
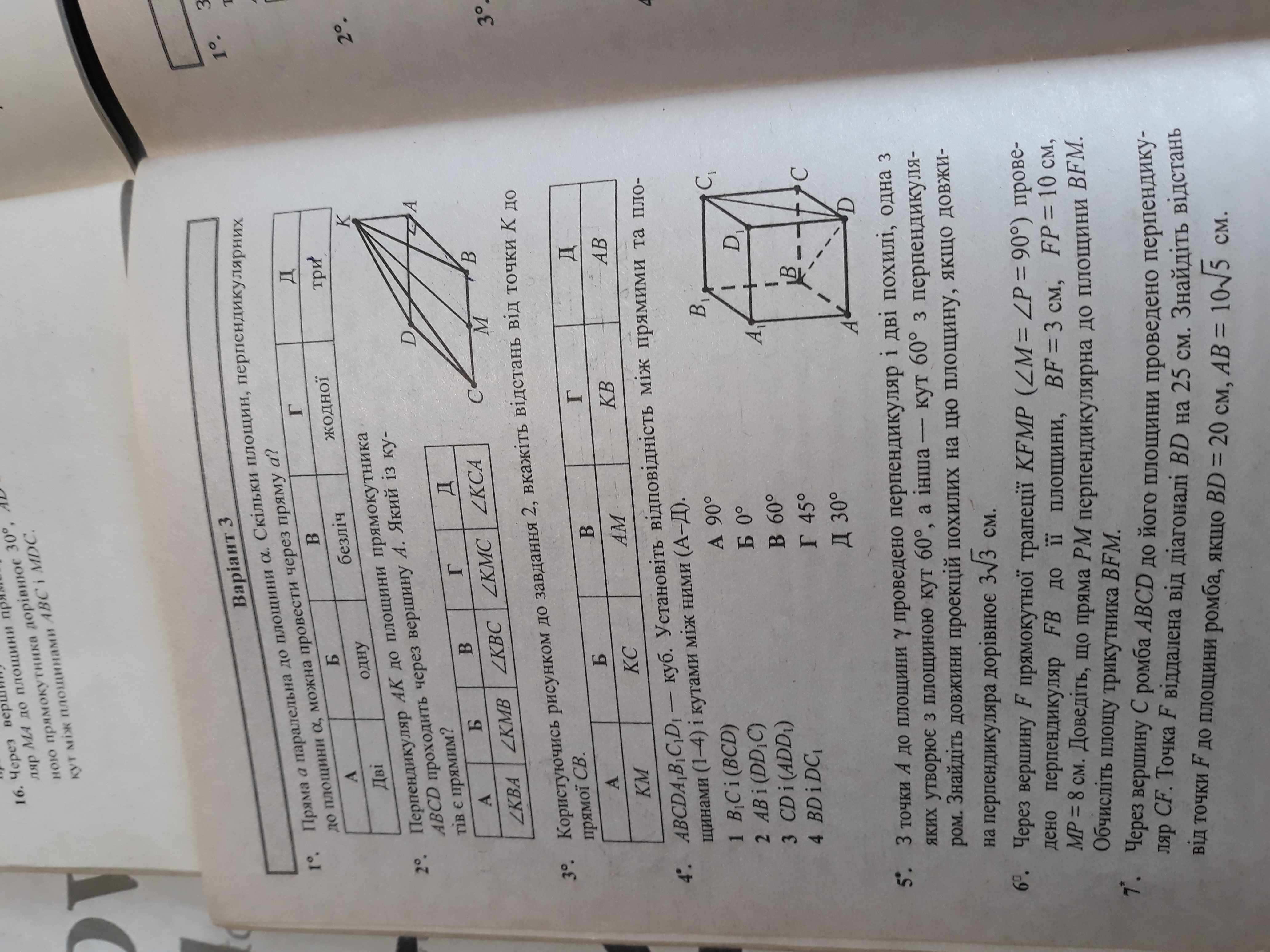
Решите 5,6,7. Спасибо)
Приложения:
Ответы
Автор ответа:
1
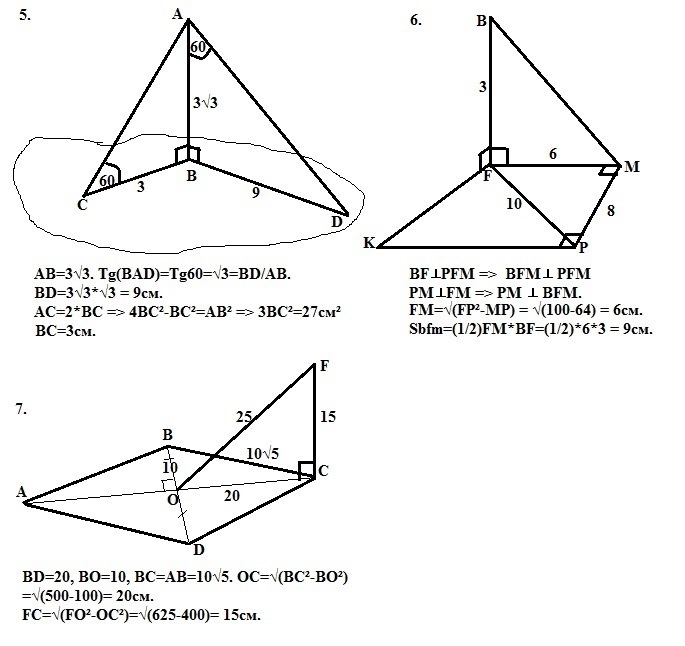
5. AB=3√3. В прямоугольном треугольнике АВD: <BAD=60°.
Tg60=√3. Tg(BAD)=BD/AB,
BD=3√3*√3 = 9см.
АС=2*ВС, так как катет ВС лежит против угла 30° в прямоугольном треугольнике АВС. По Пифагору: 4ВС²-ВС²=АВ² или 3ВС²=27см².
ВС=3см.
6. Прямая BF, лежащая в плоскости ВFM, перпендикулярна плоскости РFM (дано).Значит плоскости BFM и PFM перпендикулярны.
Прямая РМ, лежащая в плоскости РFM, перпендикулярна прямой FM (дано), лежащей в плоскости ВFM, а прямая FM - линия пересечения этих плоскостей. Следовательно, прямая РМ перпендикулярна плоскости BFM. Что и требовалось доказать.
FM=√(FP²-MP) = √(100-64) = 6см.
Sbfm=(1/2)FM*BF=(1/2)*6*3 = 9см.
7. Диагонали ромба перпендикулярны и точкой пересечения О делятся пополам. Расстояние от точки F до прямой BD - перпендикуляр FO к этой прямой. Расстояние от точки F до плоскости ромба - перпендикуляр FC к плоскости.
BD=20, BO=10, BC=AB=10√5. ОС=√(ВС²-ВО²)=√(500-100)= 20см.
FC=√(FO²-ОС²)=√(625-400)= 15см.
Tg60=√3. Tg(BAD)=BD/AB,
BD=3√3*√3 = 9см.
АС=2*ВС, так как катет ВС лежит против угла 30° в прямоугольном треугольнике АВС. По Пифагору: 4ВС²-ВС²=АВ² или 3ВС²=27см².
ВС=3см.
6. Прямая BF, лежащая в плоскости ВFM, перпендикулярна плоскости РFM (дано).Значит плоскости BFM и PFM перпендикулярны.
Прямая РМ, лежащая в плоскости РFM, перпендикулярна прямой FM (дано), лежащей в плоскости ВFM, а прямая FM - линия пересечения этих плоскостей. Следовательно, прямая РМ перпендикулярна плоскости BFM. Что и требовалось доказать.
FM=√(FP²-MP) = √(100-64) = 6см.
Sbfm=(1/2)FM*BF=(1/2)*6*3 = 9см.
7. Диагонали ромба перпендикулярны и точкой пересечения О делятся пополам. Расстояние от точки F до прямой BD - перпендикуляр FO к этой прямой. Расстояние от точки F до плоскости ромба - перпендикуляр FC к плоскости.
BD=20, BO=10, BC=AB=10√5. ОС=√(ВС²-ВО²)=√(500-100)= 20см.
FC=√(FO²-ОС²)=√(625-400)= 15см.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: sofiazeltaya2008
Предмет: Физика,
автор: Bedlam1
Предмет: Математика,
автор: ibwudhwksbhshw
Предмет: Математика,
автор: масяня93