Предмет: Математика,
автор: alisafox2
Прошуууу
С 2 до 5 задания
Алгебра, применение производной
Приложения:

Ответы
Автор ответа:
0
РЕШЕНИЕ
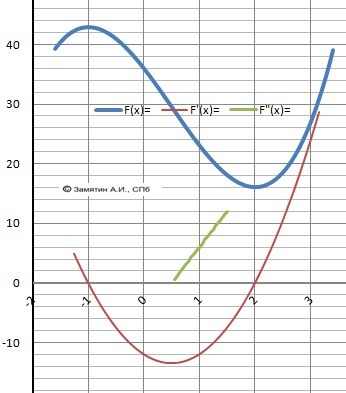
2.
Находим производную и её корни
F'(x) = 6*x² - 6x - 12 = 0
Упростили
x² - x -2 = 0
Решили квадратное уравнение
D=9,
x1 = -1, x2 = 2 - локальные экстремумы.
Вычисляем значения:
максимум = Fmax(-1) = 43
Минимум = Fmin(2) = 16
Рисунок к задаче - в подарок.
3, Y=(x²+7x)/(x-9)
Разрыв функции при х = 9 - вне интервала задачи.
Находим первую производную и экстремумы.

Корень производной - х=-3
Максимум - У(-3) = 1 - ОТВЕТ
Функция возрастающая - минимум на нижней границе интервала.
Минимум - У(-4) = 12/13 - ОТВЕТ
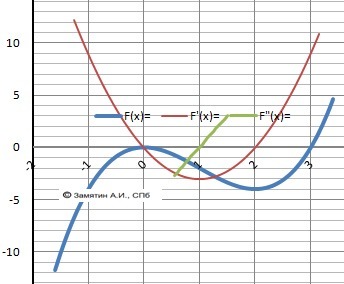
4, Исследовать функцию -
Y=x³ - 3*x².
Первая производная
Y'(x) = 3*x² - 6x = 3*x*(x-2)
Экстремумы.
Макс - Y(0) = 0
Мин - Y(2) = -4
Рисунок с графиком в приложении.
2.
Находим производную и её корни
F'(x) = 6*x² - 6x - 12 = 0
Упростили
x² - x -2 = 0
Решили квадратное уравнение
D=9,
x1 = -1, x2 = 2 - локальные экстремумы.
Вычисляем значения:
максимум = Fmax(-1) = 43
Минимум = Fmin(2) = 16
Рисунок к задаче - в подарок.
3, Y=(x²+7x)/(x-9)
Разрыв функции при х = 9 - вне интервала задачи.
Находим первую производную и экстремумы.
Корень производной - х=-3
Максимум - У(-3) = 1 - ОТВЕТ
Функция возрастающая - минимум на нижней границе интервала.
Минимум - У(-4) = 12/13 - ОТВЕТ
4, Исследовать функцию -
Y=x³ - 3*x².
Первая производная
Y'(x) = 3*x² - 6x = 3*x*(x-2)
Экстремумы.
Макс - Y(0) = 0
Мин - Y(2) = -4
Рисунок с графиком в приложении.
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: nneffos98
Предмет: История,
автор: ohrimenkodara70
Предмет: Физика,
автор: danamuzolevskaya
Предмет: Информатика,
автор: Mrfasb