Предмет: Алгебра,
автор: Аноним
Докажите , что при любом натуральном значении n выполняется равенство :
Приложения:
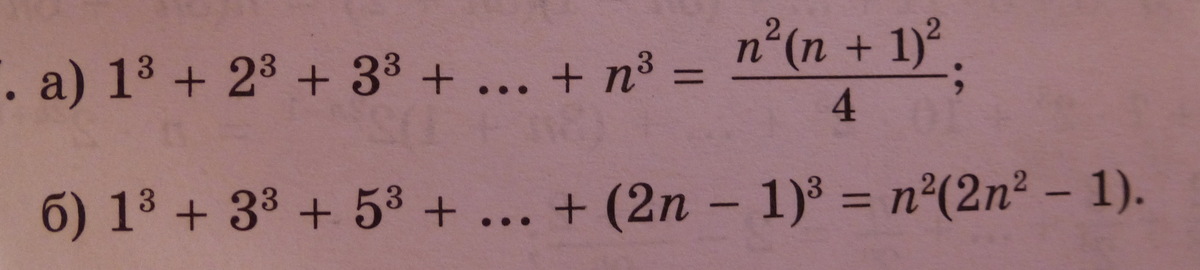
Ответы
Автор ответа:
0
Докажем с помощью математической индукций
база 1 верна
теперь переход n->n+1

переход

так как предыдущий ряд равен
то нужно доказать что
докажем

Доказано
2)
Доказано
база 1 верна
теперь переход n->n+1
переход
так как предыдущий ряд равен
то нужно доказать что
докажем
Доказано
2)
Доказано
Похожие вопросы
Предмет: История,
автор: badalovaevelina
Предмет: Математика,
автор: Ant1r0
Предмет: Математика,
автор: malinovsk56
Предмет: Алгебра,
автор: ильдар98