Question

решите уравнение с логарифмами
ответ должен быть x принадлежит (3;6]

Answer 1

Во-первых, область определения:
{ x/(x-3) > 0
{ x/(x-3) ≠ 1
{ x/3 > 0
{ x/3 ≠ 1
Решаем
{ x > 0
{ x ≠ 3
{ x - 3 > 0; x > 3
{ x ≠ x - 3 - это выполнено при любом x.
Область определения: x > 3
Далее, у логарифмов есть интересное свойство: $log_a(b)= \frac{log_c(b)}{log_c(a)}$
Причем новое основание с подходит какое угодно, лишь бы > 0 и не = 1.
Например, c = 10
$log_{ \frac{x}{x-3} }(7)= \frac{lg(7)}{lg(x/(x-3))} = \frac{lg(7)}{lg(x)-lg(x-3)}$
$log_{ \frac{x}{3} }(7)= \frac{lg(7)}{lg(x/3)} = \frac{lg(7)}{lg(x)-lg(3)}$
Подставляем в наше неравенство:
$\frac{lg(7)}{lg(x)-lg(x-3)} \leq \frac{lg(7)}{lg(x)-lg(3)}$
Делим всё на lg(7)
$\frac{1}{lg(x)-lg(x-3)} \leq \frac{1}{lg(x)-lg(3)}$
Если у дробей одинаковые числители, то чем больше знаменатель, тем меньше дробь.
lg(x) - lg(x - 3) ≥ lg(x) - lg(3)
lg(x) вычитаем слева и справа
-lg(x - 3) ≥ -lg(3)
Умножаем всё на -1, при этом меняется знак неравенства.
lg(x - 3) ≤ lg(3)
Переходим от логарифмов к числам под ними. Функция y = lg(x) возрастает, поэтому при переходе знак неравенства остается.
x - 3 ≤ 3
x ≤ 6
По области определения x > 3
Ответ: x ∈ (3; 6]

Answer 2

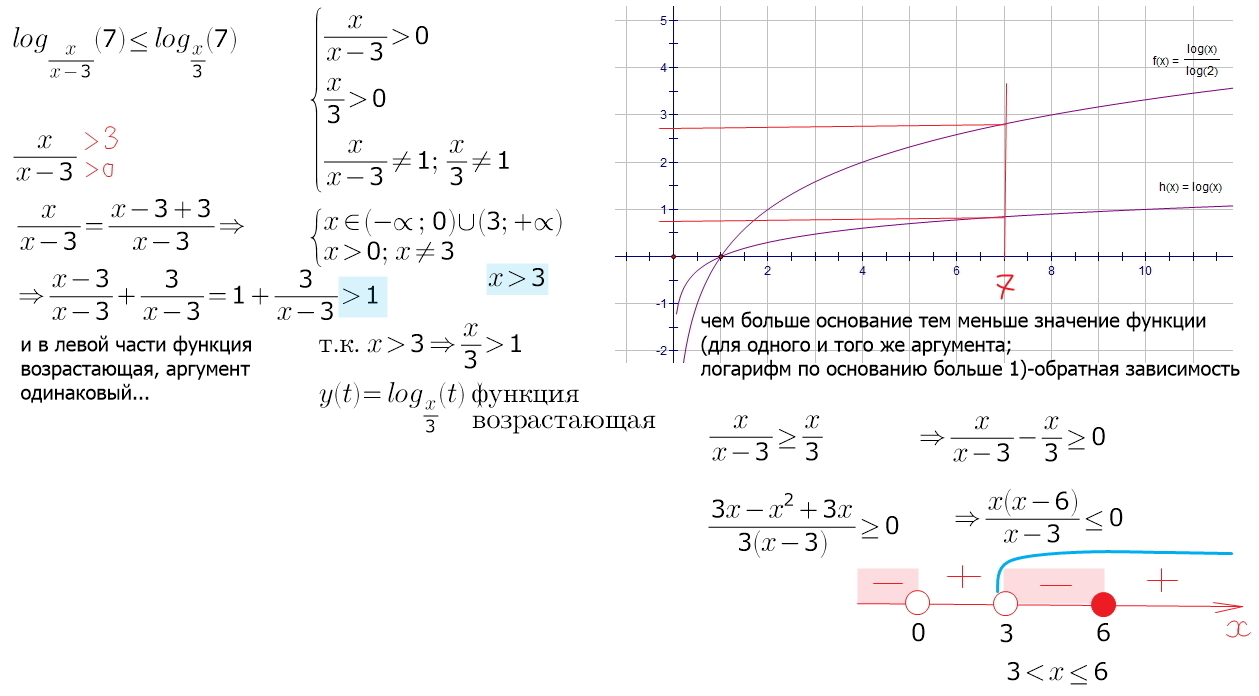
найденное ОДЗ
позволяет утверждать, что обе логарифмические функции
являются возрастающими (аргумент одинаковый), 
потому достаточно сравнить основания...