Предмет: Геометрия,
автор: OlyaGr
докажите, что средняя линия трапеции проходит через середины диагоналей. Докажите пожалуйста, но не по теореме Фалеса)
Ответы
Автор ответа:
0
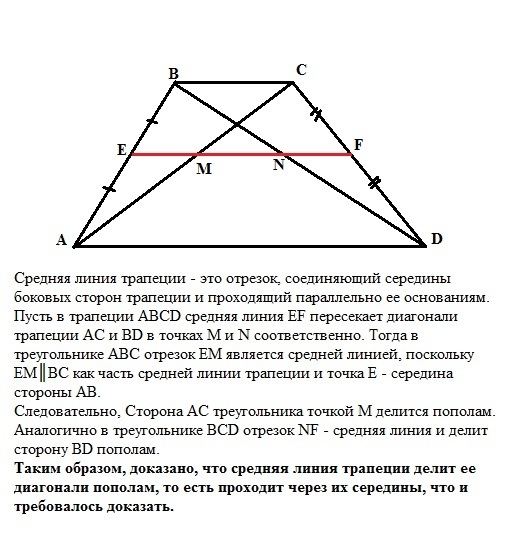
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции и проходящий параллельно ее основаниям.
Пусть в трапеции АВСD средняя линия EF пересекает диагонали трапеции АС и ВD в точках М и N соответственно. Тогда в треугольнике АВС отрезок ЕМ является средней линией, поскольку ЕМ║ВС как часть средней линии трапеции и точка Е - середина стороны АВ.
Следовательно, Сторона АС треугольника точкой М делится пополам.
Аналогично в треугольнике ВCD отрезок NF - средняя линия и делит сторону BD пополам.
Таким образом, доказано, что средняя линия трапеции делит ее диагонали пополам, то есть проходит через их середины, что и требовалось доказать.
Приложения:
Похожие вопросы