Предмет: Математика,
автор: denison88
Вычислить неопределенный интеграл
Приложения:
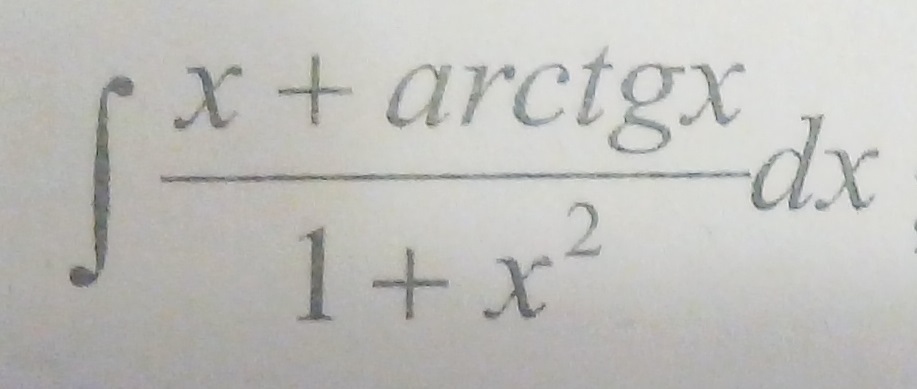
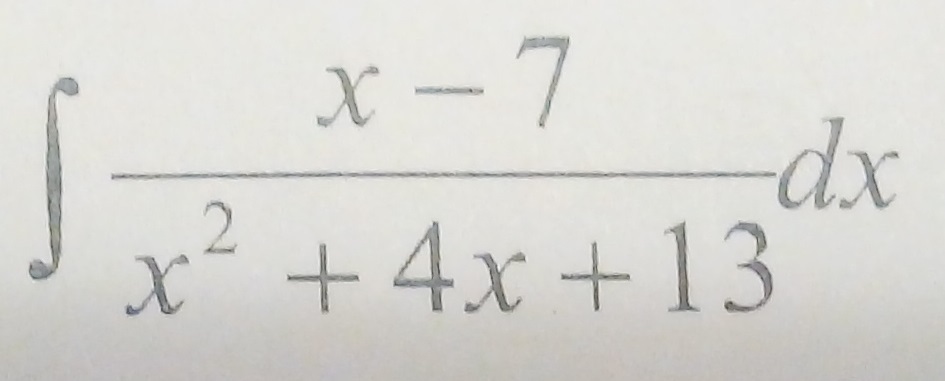
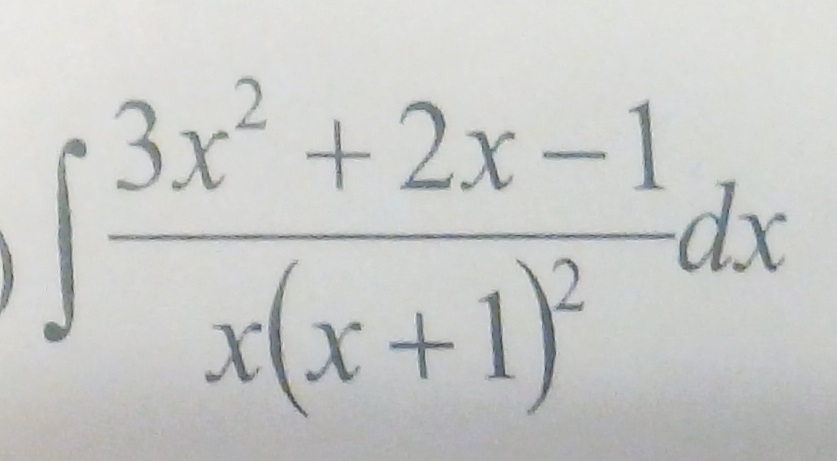
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: sinurabeknazarova425
Предмет: Физкультура и спорт,
автор: kostyryayekaterina
Предмет: Математика,
автор: katya6269
Предмет: Математика,
автор: кек123123