Question

1 из внешних углов прямоугольного треугольника равен 120 градусов. Найдите большую имеющие стороны треугольника , если их сумма равна 12 см.

Answer 1

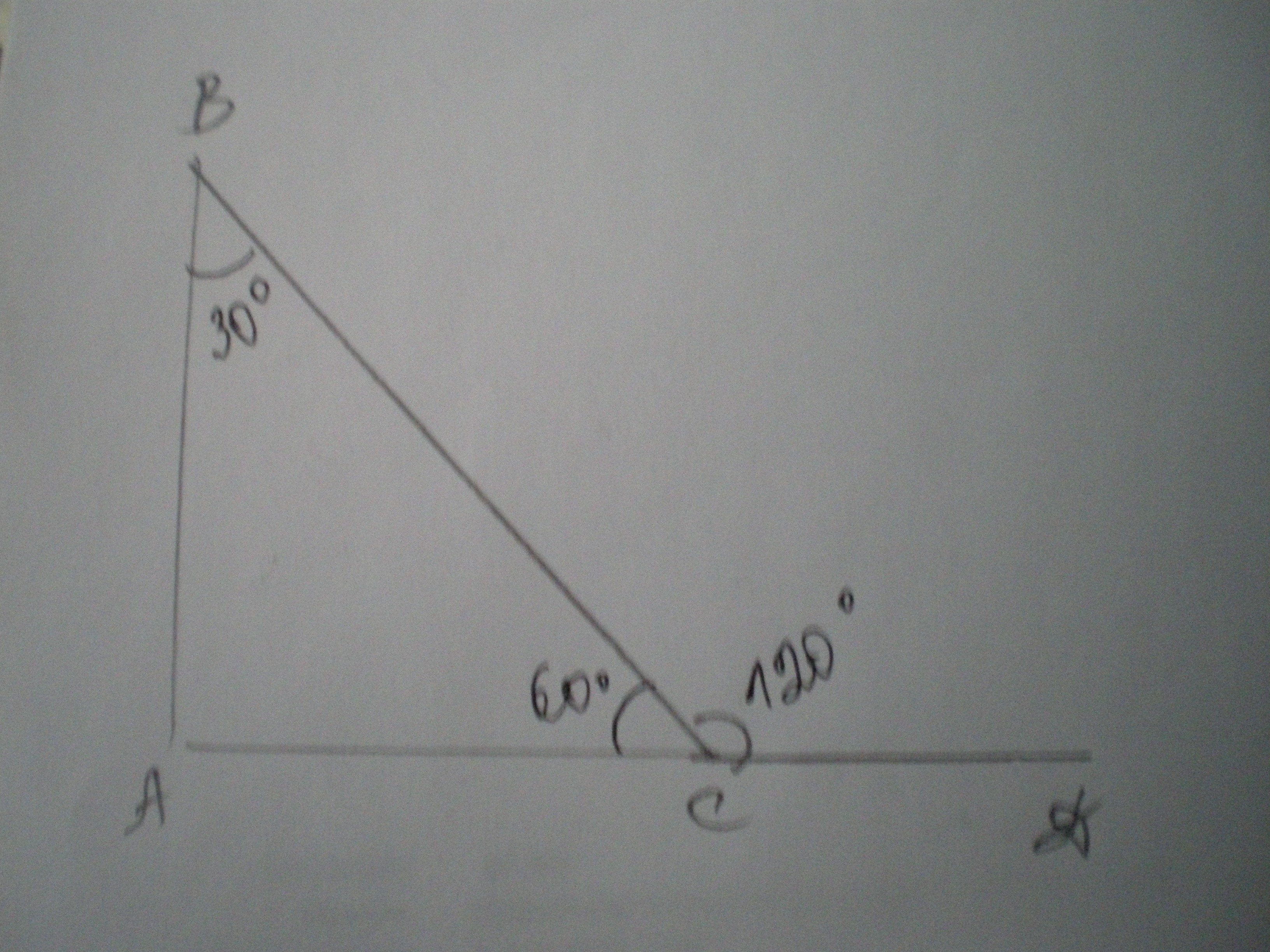
Угол АСД=120 градусов, угол АСВ=180-120=60 градусов,
угол В=90-60=30 градусов.
Большая сторона лежит против большего угла, это гипотенуза ВС. Меньшая сторона АС, т.к. она лежит против меньшего угла.
По условию АС+ВС=12 см.
при этом АС=1\2 ВС, как катет, лежащий против угла 30 градусов.
Имеем систему уравнений:
АС+ВС=12
АС=ВС\2

АС=12-ВС
АС=ВС\2

12-ВС=ВС\2
2(12-ВС)=ВС
24-2ВС=ВС
3ВС=24
ВС=8 см
АС=12-8=4 см

Ответ: 8 см, 4 см.