Question

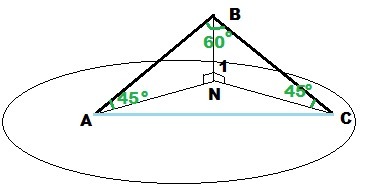
Из точки В, которая размещена от плоскости на расстоянии 1, проведено две наклонные, которые образуют с плоскостью углы 45 градусов, а между собой - 60 градусов. Найти квадрат расстояния между концами наклонных.

Answer 1

Дано: AB, BC - наклонные к плоскости
BN = 1;   ∠BAN = ∠BCN = 45°;     ∠ABC = 60°
Найти: AC²

ΔABN = ΔCBN по двум углам: прямому и 45°  ⇒ AN=NC; AB=BC
∠ABN = 90°-∠BAN = 90°- 45° = 45°  ⇒
ΔABN = ΔCBN - прямоугольные равнобедренные ⇒
AN = NC = NB = 1
Теорема Пифагора
AB² = AN² + NB² = 1+1 = 2

ΔABC - равнобедренный, ∠ABC = 60° ⇒
∠BAC = ∠BCA = (180°-60°)/2 = 60° ⇒
ΔABC - равносторонний  ⇒
AC² = BC² = AB² = 2

Ответ: квадрат расстояния  2