Question

Пожалуйста помогите
Напишите уравнение прямой, проходящей через первую четверть и отсекающей на осях координат равные отрезки, если длина отрезка этой прямой, заключенного между осями координат, равна 5√2.

Answer 1

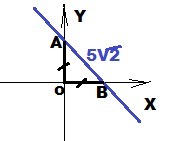
AB = 5√2;   OA = OB  - по условию
ΔOAB - прямоугольный равнобедренный
Теорема Пифагора
OA² + OB² = AB²   ⇒    2OA² = AB²
2OA² = (5√2)²
2OA² = 50   ⇒   OA² = 25    ⇒     OA = OB = 5
Координаты точек  А (0; 5),  В (5; 0)
Уравнение прямой y = kx+b
Для точки А:   5 = k*0 + b;    b = 5
Для точки В:   0 = k*5 + b;   5k = -b;     k = -b/5;
k = -5/5 = -1

Уравнение прямой y = -x + 5