Предмет: Алгебра,
автор: makoron
Докажите что при любом натуральном значении n выполняется равентсво:
Приложения:
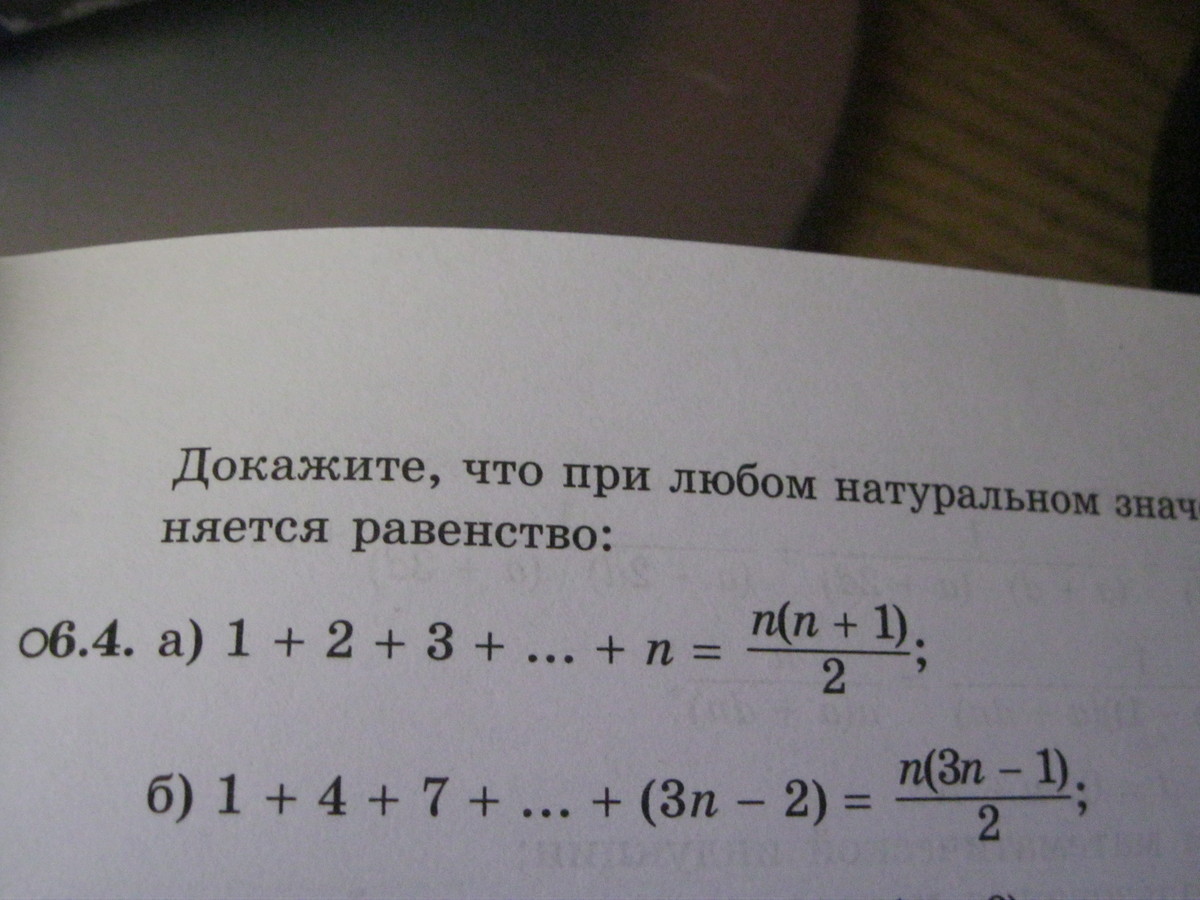
Ответы
Автор ответа:
0
При n=1
Пусть при n=k
Докажем, что при n=k+1 равенство будет также верно
При n=1
Пусть при n=k
Докажем, что при n=k+1 равенство будет также верно
Автор ответа:
0
1) Можно с помощью суммы арифметической прогрессии


Похожие вопросы
Предмет: Математика,
автор: nadirovafatima329
Предмет: Химия,
автор: ssssssssssarra
Предмет: Математика,
автор: olgamalakhova2013
Предмет: Литература,
автор: артем223ка
Предмет: Математика,
автор: Марго20010802