Предмет: Математика,
автор: Yana2502
Тригонометрия:
Известно, что ctgx=3/4, x принадлежит [П;3П/2] вычисл: cos/sin/tg/ctg x/2
Приложения:
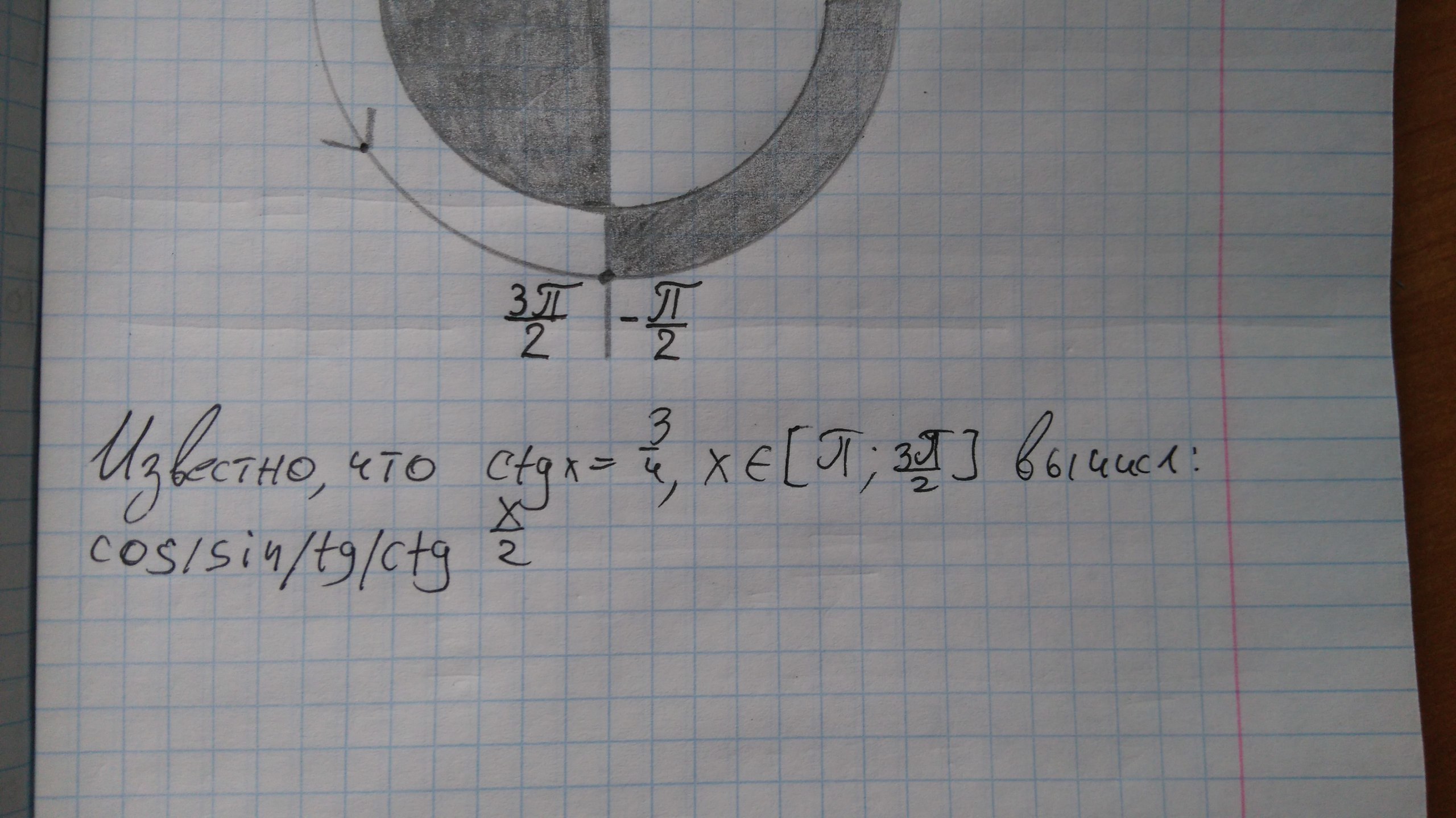
Ответы
Автор ответа:
2
- III четверть
III четверть : cos x < 0; sin x < 0; tg x > 0
II четверть :
Похожие вопросы
Предмет: Биология,
автор: dilnaraserikbay44
Предмет: Математика,
автор: janka91baik
Предмет: История,
автор: glebovadaska70
Предмет: Математика,
автор: абвгдеёжз2